题目内容

已知{an}是等比数列，a6=2，a3=
1
4
，则公比q等于（　　）
A、-
1
2
B、-2
C、2
D、
1
2
考点：等比数列的性质
专题：等差数列与等比数列
分析：等比数列{an}中，
am
an
=qm-n，由此根据已知条件能求出公比q．
解答： 解：∵{an}是等比数列，a6=2，a3=
1
4
，
∴q3=
a6
a3
=
2
1
4
=8，
解得q=2．
故选：C．
点评：本题考查数列的公比的求法，是基础题，解题时要熟练掌握等比数列的通项公式．
练习册系列答案
相关题目
已知点M（3，1），直线ax-y+4=0及圆（x-1）2+（y-2）2=4．
（1）求过M点的圆的切线方程；
（2）若直线ax-y+4=0与圆相切，求a的值．
已知f（cos
x
2
）=3cosx+2，则f（sin
π
8
）=
 
．
已知复数z的模|z|=2，那么|z+5+i|的最大值是
 
．
曲线x2+y2+y+m=0和它关于直线x+2y-1=0的对称曲线总有四条公切线，则m的取值范围
 
．
不等式2x2+mx+n＞0的解集是{x|x＞3或x＜-2}，则二次函数y=2x2+mx+n的表达式是（　　）
A、y=2x2+2x+12
B、y=2x2-2x+12
C、y=2x2+2x-12
D、y=2x2-2x-12
所有与角α终边相同的角，连同角α在内，可构成的一个集合S是（　　）
A、{β|β=α+k•180°，k∈Z}
B、{β|β=α+k•360°，k∈Z}
C、{β|β=α+k•180°，k∈R}
D、{β|β=α+k•360°，k∈R}
已知直线y=x+b与曲线x2+y2=1（x＞0）有交点，则（　　）
A、-1＜b＜1
B、-1＜b＜
2
C、-
2
≤b≤
2
D、-
2
≤b＜1
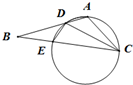选修4-1：几何证明选讲
如图，在△ABC中，CD是∠ACB的角平分线，△ACD的外接圆交BC于E，AB=2AC．
（Ⅰ）求证：BE=2AD；
（Ⅱ）若AC=1，EC=2，求AD的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网