题目内容
已知数列{an}的前n项和为Sn,a1=t(t≠-1),an+1-Sn=n.
(Ⅰ) 当t为何值时,数列{an+1}是等比数列?
(Ⅱ) 设数列{bn}的前n项和为Tn,b1=1,点(Tn+1,Tn)在直线
-
=
上,在(Ⅰ)的条件下,若不等式
+
+…+
≥m-
对于n∈N*恒成立,求实数m的最大值.
(Ⅰ) 当t为何值时,数列{an+1}是等比数列?
(Ⅱ) 设数列{bn}的前n项和为Tn,b1=1,点(Tn+1,Tn)在直线
| x |
| n+1 |
| y |
| n |
| 1 |
| 2 |
| b1 |
| a1+1 |
| b2 |
| a2+1 |
| bn |
| an+1 |
| 9 |
| 2+2an |
考点:数列与不等式的综合
专题:等差数列与等比数列,不等式的解法及应用
分析:(Ⅰ) 由条件an+1-Sn=n,令n=n-1得an-Sn-1=n-1(n≥2),两式相减得数列递推公式an+1=2an+1,转化为an+1+1=2(an+1)(n≥2)求a2,然后利用数列{an+1}是等比数列,再求t即可;
(Ⅱ)由点(Tn+1,Tn)在直线
-
=
上求出{
}是等差数列且Tn=
,然后求出bn=n,连同an=2n-1-1代入不等式化简.不等式的左边为等比数列前n项和令其为所Rn,利用错位相减法求出Rn=4-
,则原不等式为Rn≥m-
恒成立,即4-
≥m恒成立,利用数列的增减性求解.
(Ⅱ)由点(Tn+1,Tn)在直线
| x |
| n+1 |
| y |
| n |
| 1 |
| 2 |
| Tn |
| n |
| n(n+1) |
| 2 |
| n+2 |
| 2n-1 |
| 9 |
| 2n |
| 2n-5 |
| 2n |
解答:
解:(Ⅰ)由an+1-Sn=n,得an-Sn-1=n-1(n≥2),
两式相减得an+1-an-(Sn-Sn-1)=1,即an+1=2an+1,
所以an+1+1=2(an+1)(n≥2),
由a1=t及an+1-Sn=n,得a2=t+1,
因为数列{an+1}是等比数列,所以只需要
=
=2,解得t=0,此时,数列{an+1}是以a1+1=1为首项,2为公比的等比数列.
(Ⅱ)由(Ⅰ)得an=2n-1-1,因为点(Tn+1,Tn)在直线
-
=
上,所以
-
=
,
故{
}是以
=1为首项,
为公差的等差数列,则
=1+
(n-1),所以Tn=
,
当n≥2时,bn=Tn-Tn-1=
-
=n,b1=1满足该式,所以bn=n.
不等式
+
+…+
≥m-
,即为1+
+
+…+
≥m-
,
令Rn=1+
+
+…+
,则
Rn=
+
+
+…+
,两式相减得(1-
)Rn=1+
+
+
+…+
-
=2-
,所以Rn=4-
.
由Rn≥m-
恒成立,即4-
≥m恒成立,又(4-
)-(4-
)=
,
故当n≤3时,{4-
}单调递减;当n≥4时,{4-
}单调递增,
当n=3时,4-
=
;当n=4时,4-
=
,则4-
的最小值为
,所以实数m的最大值是
.
两式相减得an+1-an-(Sn-Sn-1)=1,即an+1=2an+1,
所以an+1+1=2(an+1)(n≥2),
由a1=t及an+1-Sn=n,得a2=t+1,
因为数列{an+1}是等比数列,所以只需要
| a2+1 |
| a1+1 |
| t+2 |
| t+1 |
(Ⅱ)由(Ⅰ)得an=2n-1-1,因为点(Tn+1,Tn)在直线
| x |
| n+1 |
| y |
| n |
| 1 |
| 2 |
| Tn+1 |
| n+1 |
| Tn |
| n |
| 1 |
| 2 |
故{
| Tn |
| n |
| T1 |
| 1 |
| 1 |
| 2 |
| Tn |
| n |
| 1 |
| 2 |
| n(n+1) |
| 2 |
当n≥2时,bn=Tn-Tn-1=
| n(n+1) |
| 2 |
| (n-1)n |
| 2 |
不等式
| b1 |
| a1+1 |
| b2 |
| a2+1 |
| bn |
| an+1 |
| 9 |
| 2+2an |
| 2 |
| 2 |
| 3 |
| 22 |
| n |
| 2n-1 |
| 9 |
| 2n |
令Rn=1+
| 2 |
| 2 |
| 3 |
| 22 |
| n |
| 2n-1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 22 |
| 3 |
| 23 |
| n |
| 2n |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n-1 |
| n |
| 2n |
| n+2 |
| 2n |
| n+2 |
| 2n-1 |
由Rn≥m-
| 9 |
| 2n |
| 2n-5 |
| 2n |
| 2n-3 |
| 2n+1 |
| 2n-5 |
| 2n |
| 2n-7 |
| 2n+1 |
故当n≤3时,{4-
| 2n-5 |
| 2n |
| 2n-5 |
| 2n |
当n=3时,4-
| 2×3-5 |
| 23 |
| 31 |
| 8 |
| 2×4-5 |
| 24 |
| 61 |
| 16 |
| 2n-5 |
| 2n |
| 61 |
| 16 |
| 61 |
| 16 |
点评:本题是典型的数列题,形式复杂,但规律性强,第一问属基础技巧,知Sn,an混合式求递推公式再求通项,第二问较难,求出bn,代入不等式求解,千万不要怕复杂,克服畏惧心理,沉着答题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知m是平面α的一条斜线,点A∉α,为l过点A的一条动直线,那么下列情形可能出现的是( )
| A、l⊥m且l∥m |
| B、l∥m且l⊥α |
| C、l⊥m且l⊥α |
| D、l∥m且l∥α |
函数f(x)=x3+ax2+x在(0,+∞)有两个极值点,则实数a的取值范围是( )
A、(-∞,
| ||||
B、(-
| ||||
C、(
| ||||
D、(-∞,-
|
下列向量是单位向量的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
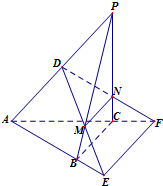 如图,在三棱锥P-ABC中,CP,CA,CB两两垂直且相等,过PA的中点D作平面α∥BC,且α分别交PB,PC于M,N,交AB,AC的延长线于E,F.
如图,在三棱锥P-ABC中,CP,CA,CB两两垂直且相等,过PA的中点D作平面α∥BC,且α分别交PB,PC于M,N,交AB,AC的延长线于E,F.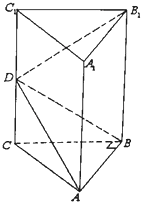 如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,CC1=2AB=2BC=2,D是CC1中点
如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,CC1=2AB=2BC=2,D是CC1中点