Question

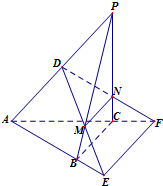如图，在三棱锥P-ABC中，CP，CA，CB两两垂直且相等，过PA的中点D作平面α∥BC，且α分别交PB，PC于M，N，交AB，AC的延长线于E，F．
（Ⅰ）求证：EF⊥平面PAC；
（Ⅱ）若AB=2BE，求二面角P-DM-N的余弦值．

Answer 1

考点：用空间向量求平面间的夹角,直线与平面垂直的判定

专题：计算题,空间位置关系与距离,空间角

分析：（Ⅰ）运用线面垂直的判定和性质定理，以及线面平行的性质定理，即可得证；
（Ⅱ）以CA，CB，CP分别为x，y，z轴建立空间直角坐标系，并设BC=2，求出点A，B，P，D，E，F的坐标，设平面PAB的法向量和平面DEF的法向量，由向量垂直的条件：数量积为0，即可得到法向量，再由向量的夹角公式，即可得到所求二面角的余弦值．

解答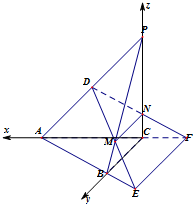： （Ⅰ）证明：由BC⊥PC，BC⊥AC可知：BC⊥平面PAC，
又因为平面α∥BC，平面AEF过BC且与平面α交于EF，
所以EF∥BC．
故EF⊥平面PAC； 　
（Ⅱ）以CA，CB，CP分别为x，y，z轴建立空间直角坐标系，
并设BC=2．则A（2，0，0），B（0，2，0），P（0，0，2），
设平面PAB的法向量

n1

=(x1，y1，z1)，
由

n1

•

PA

=0，

n1

•

PB

=0，可求得

n1

=(1，1，1)，
D（1，0，1），E（-1，3，0），F（-1，0，0），
设平面DEF的法向量

n2

=(x，y，z)，
由

n2

•

DE

=0，

n2

•

FE

=0，可得

n2

=(-1，0，2)，
cos?

n1

，

n2

＞=

n1 • n2

| n1 |•| n2 |

=

15

15

．
二面角P-DM-N的余弦值为

15

15

．

点评：本题考查空间位置关系：平行和垂直，考查线面垂直的判定和性质定理，以及线面平行的性质定理，考查空间二面角的求法，主要是运用向量法解决，考查运算能力，属于中档题．