题目内容
16.设变量x,y满足约束条件$\left\{\begin{array}{l}x-y+1≥0\\ x+y-1≥0\\ 3x-y-3≤0\end{array}\right.$则目标函数z=4x+y的最大值为( )| A. | 4 | B. | 11 | C. | 12 | D. | 14 |
分析 利用线性规划的内容作出不等式组对应的平面区域,然后由z=4x+y得y=-4x+z,根据平移直线确定目标函数的最大值.
解答 解:作出不等式组对应的平面区域如图: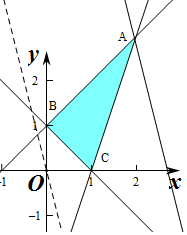
由z=4x+y得y=-4x+z,平移直线y=-4x+z,
由图象可知当直线经过点A时,直线的截距最大,此时Z最大,
由$\left\{\begin{array}{l}{x-y+1=0}\\{3x-y-3=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$,即A(2,3),
代入z=4x+y得最大值为z=4×2+3=11.
故选:B.
点评 本题主要考查二元一次不等式组表示平面区域的知识,以及线性规划的基本应用,利用数形结合是解决此类问题的关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
6.函数y=ex(e是自然对数的底数)在点(0,1)处的切线方程是( )
| A. | y=x-1 | B. | y=x+1 | C. | y=-x-1 | D. | y=-x+1 |
4.已知F1,F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的两个焦点,PQ是经过F1且垂直于x轴的双曲线的弦,若∠PF2Q=90°,则双曲线的离心率为( )
| A. | 2 | B. | $2\sqrt{2}$ | C. | $\sqrt{2}-1$ | D. | $1+\sqrt{2}$ |
11.已知函数$f(x)=\sqrt{x}sinx$,则f'(π)=( )
| A. | $\sqrt{π}$ | B. | $-\sqrt{π}$ | C. | $\frac{{\sqrt{π}}}{2π}$ | D. | $\frac{{\sqrt{2π}}}{2π}$ |
1.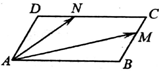 如图,在平行四边形ABCD中,$∠BAD=\frac{π}{3}$,AB=2,AD=1,若M、N分别是边BC、CD上的点,且满足$\frac{BM}{BC}=\frac{NC}{DC}=λ$,其中λ∈[0,1],则$\overrightarrow{AM}•\overrightarrow{AN}$的取值范围是( )
如图,在平行四边形ABCD中,$∠BAD=\frac{π}{3}$,AB=2,AD=1,若M、N分别是边BC、CD上的点,且满足$\frac{BM}{BC}=\frac{NC}{DC}=λ$,其中λ∈[0,1],则$\overrightarrow{AM}•\overrightarrow{AN}$的取值范围是( )
 如图,在平行四边形ABCD中,$∠BAD=\frac{π}{3}$,AB=2,AD=1,若M、N分别是边BC、CD上的点,且满足$\frac{BM}{BC}=\frac{NC}{DC}=λ$,其中λ∈[0,1],则$\overrightarrow{AM}•\overrightarrow{AN}$的取值范围是( )
如图,在平行四边形ABCD中,$∠BAD=\frac{π}{3}$,AB=2,AD=1,若M、N分别是边BC、CD上的点,且满足$\frac{BM}{BC}=\frac{NC}{DC}=λ$,其中λ∈[0,1],则$\overrightarrow{AM}•\overrightarrow{AN}$的取值范围是( )| A. | [0,3] | B. | [1,4] | C. | [2,5] | D. | [1,7] |
8.设集合A={x|x2-x-6<0},B={x|-3≤x≤1},则A∪B等于( )
| A. | [-2,1) | B. | (-2,1] | C. | [-3,3) | D. | (-3,3] |
5.已知圆锥的底面半径为1,侧面展开图的圆心角为60°,则此圆锥的表面积为( )
| A. | 3π | B. | 5π | C. | 7π | D. | 9π |
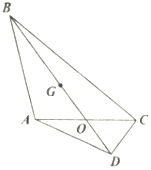 如图,在平面四边形ABCD中,$\overrightarrow{BA}•\overrightarrow{BC}=32$.
如图,在平面四边形ABCD中,$\overrightarrow{BA}•\overrightarrow{BC}=32$.