题目内容
若数列{An}满足An+1=An2,则称数列{An}为“平方递推数列”.已知数列{an}中,a1=9,点(an,an+1)在函数f(x)=x2+2x的图象上,其中n为正整数.
(Ⅰ)证明数列{an+1}是“平方递推数列”,且数列{lg(an+1)}为等比数列;
(Ⅱ)设(Ⅰ)中“平方递推数列”的前n项积为Tn,即Tn=(a1+1)(a2+1)…(an+1),求lgTn;
(Ⅲ)在(Ⅱ)的条件下,记bn=
,求数列{bn}的前n项和Sn,并求使Sn>4026的n的最小值.
(Ⅰ)证明数列{an+1}是“平方递推数列”,且数列{lg(an+1)}为等比数列;
(Ⅱ)设(Ⅰ)中“平方递推数列”的前n项积为Tn,即Tn=(a1+1)(a2+1)…(an+1),求lgTn;
(Ⅲ)在(Ⅱ)的条件下,记bn=
| lgTn |
| lg(an+1) |
考点:数列与不等式的综合,数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件推导出an+1+1=(an+1)2,从而能证明{an+1}是“平方递推数列”,对an+1+1=(an+1)2两边取对数能证明数列{lg(an+1)}是等比数列.
(Ⅱ)由(Ⅰ)知 lg(an+1)=lg(a1+1)•2n-1=2n-1,从而得到lgTn=20+2+22+…+2n-1,由此利用等比数列求和公式能求出结果.
(Ⅲ)由bn=
=
=2-(
)n-1,求出Sn=2n-
=2n-2+
,由此能求出使Sn>4026的n的最小值.
(Ⅱ)由(Ⅰ)知 lg(an+1)=lg(a1+1)•2n-1=2n-1,从而得到lgTn=20+2+22+…+2n-1,由此利用等比数列求和公式能求出结果.
(Ⅲ)由bn=
| lgTn |
| lg(an+1) |
| 2n-1 |
| 2n-1 |
| 1 |
| 2 |
1-
| ||
1-
|
| 1 |
| 2n-1 |
解答:
(Ⅰ)证明:∵点(an,an+1)在函数f(x)=x2+2x的图象上,
∴an+1=an2+2an,
∴an+1+1=(an+1)2,
∴{an+1}是“平方递推数列”.…(2分)
对an+1+1=(an+1)2两边取对数得lg(an+1+1)=2lg(an+1),
∴数列{lg(an+1)}是以{lg(a1+1)}为首项,2为公比的等比数列.…(4分)
(Ⅱ)解:由(Ⅰ)知 lg(an+1)=lg(a1+1)•2n-1=2n-1…(5分)
∴lgTn=lg(a1+1)(a2+1)…(an+1)
=lg(a1+1)+lg(a2+1)+…+lg(an+1)
=20+2+22+…+2n-1
=
=2n-1.…(8分)
(Ⅲ)解:∵bn=
=
=2-(
)n-1…(9分)
∴Sn=2n-
=2n-2+
…(10分)
又Sn>4026,即2n-2+
>4026,n+
>2014…(11分)
又0<
<1,∴nmin=2014.…(12分)
∴an+1=an2+2an,
∴an+1+1=(an+1)2,
∴{an+1}是“平方递推数列”.…(2分)
对an+1+1=(an+1)2两边取对数得lg(an+1+1)=2lg(an+1),
∴数列{lg(an+1)}是以{lg(a1+1)}为首项,2为公比的等比数列.…(4分)
(Ⅱ)解:由(Ⅰ)知 lg(an+1)=lg(a1+1)•2n-1=2n-1…(5分)
∴lgTn=lg(a1+1)(a2+1)…(an+1)
=lg(a1+1)+lg(a2+1)+…+lg(an+1)
=20+2+22+…+2n-1
=
| 1•(1-2n) |
| 1-2 |
(Ⅲ)解:∵bn=
| lgTn |
| lg(an+1) |
| 2n-1 |
| 2n-1 |
| 1 |
| 2 |
∴Sn=2n-
1-
| ||
1-
|
| 1 |
| 2n-1 |
又Sn>4026,即2n-2+
| 1 |
| 2n-1 |
| 1 |
| 2n |
又0<
| 1 |
| 2n |
点评:本题考查“平方递推数列”和等比数列的证明,考查数列前n项和的求法,考查最小值的求法,解题时要认真审题,注意等比数列前n项和公式的合理运用.

练习册系列答案
相关题目
等差数列{an}中,若
=
,则
=( )
| a7 |
| a5 |
| 9 |
| 13 |
| S13 |
| S9 |
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
已知数列{an}是等比数列,且a1+a3=-3,a2a4=4,则公比q的值是( )
A、
| ||
| B、-2 | ||
C、±
| ||
| D、±2 |
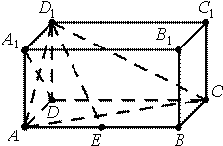 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.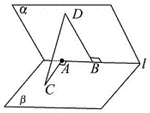 如图,60°的二面角的棱上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB,已知AB=4,AC=6,BD=8,则CD的长为
如图,60°的二面角的棱上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB,已知AB=4,AC=6,BD=8,则CD的长为