题目内容

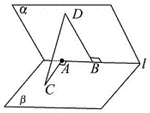如图，60°的二面角的棱上有A，B两点，直线AC，BD分别在这个二面角的两个半平面内，且都垂直于AB，已知AB=4，AC=6，BD=8，则CD的长为
 
．
考点：点、线、面间的距离计算
专题：计算题,空间位置关系与距离
分析：由已知可得
CD
 • 
AB
 =0， 
AB
 • 
BD
 =0，
CD
=
CA
+
AB
+
BD
，利用数量积的性质即可得出．
解答： 解：由条件，知
CD
 • 
AB
 =0， 
AB
 • 
BD
 =0，
CD
=
CA
+
AB
+
BD
．
所以|
CD
|2=|
CA
|2+|
AB
|2+|
BD
|2+2
CA
•
AB
+2
AB
•
BD
+2
CA
•
BD

=62+42+82+2×6×8cos120°=68
所以CD=2
17
．
故答案为：2
17
．
点评：本题考查面面角，考查空间距离的计算，熟练掌握向量的运算和数量积运算是解题的关键．
练习册系列答案
相关题目
若数列{An}满足An+1=An2，则称数列{An}为“平方递推数列”．已知数列{an}中，a1=9，点（an，an+1）在函数f（x）=x2+2x的图象上，其中n为正整数．
（Ⅰ）证明数列{an+1}是“平方递推数列”，且数列{lg（an+1）}为等比数列；
（Ⅱ）设（Ⅰ）中“平方递推数列”的前n项积为Tn，即Tn=（a1+1）（a2+1）…（an+1），求lgTn；
（Ⅲ）在（Ⅱ）的条件下，记bn=
lgTn
lg(an+1)
，求数列{bn}的前n项和Sn，并求使Sn＞4026的n的最小值．
已知函数f（x）=ax3+bx2+cx+d（a≠0）的对称中心为M（x0，y0），记函数f（x）的导函数为f′（x），f′（x）的导函数为f″（x），则有f″（x0）=0．若函数f（x）=x3-3x2，则可求得f（
1
2013
）+f（
2
2013
）+…+f（
4024
2013
）+f（
4025
2013
）
 
．
已知数列{an}的通项公式为an=25-n，数列{bn}的通项公式为bn=n+k，设cn=
bn，an≤bn
an，an＞bn
若在数列{cn}中，c5≤cn对任意n∈N*恒成立，则实数k的取值范围是
 
．
设函数f（x）=
x
 x≥0
-x
  x＜0
，若f（a）+f（-1）=3，则实数a=
 
．
在(
x
+
a
x
)6（a＞0）的展开式中含常数项的系数是60，则
∫
a
0
sinxdx的值为
 
．
设函数f（x）的定义域为D，如果存在正实数k，使对任意x∈D，都有x+k∈D，且f（x+k）＞f（x）恒成立，则称函数f（x）为D上的“k型增函数”．已知f（x）是定义在R上的奇函数，且当x＞0时，f（x）=|x-a|-2a，若f（x）为R上的“2014型增函数”，则实数a的取值范围是
 
．
长方体ABCD-A1B1C1D1中，AB=3，BC=2，AA1=1，一绳子从A沿着表面拉到C1的最短距离是（　　）
A、
26
B、2
5
C、3
2
D、
14
已知二项式(
5x
+
1
2x
)m的展开式中第2项为常数项t，其中m∈N*，且展开式按x的降幂排列．
（Ⅰ）求m及t的值．
（Ⅱ）数列{an}中，a1=t，an=tan-1-，n∈N*，求证：an-3能被4整除．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网