题目内容

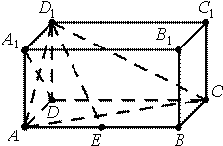如图，在长方体ABCD-A1B1C1D1中，AD=AA1=1，AB=2，点E在棱AB上移动．
（1）求异面直线D1E与A1D所成角．
（2）（文）当E为AB中点时，求点E到平面ACD1的距离．
考点：点、线、面间的距离计算,异面直线及其所成的角
专题：综合题,空间位置关系与距离,空间角
分析：（1）以D为原点DA、DC、DD1为x，y，z轴，建立坐标系，证明
DA1
•
D1E
=0，即可求异面直线D1E与A1D所成角；
（2）由VD1-AEC=VE-ACD1，即可求点E到平面ACD1的距离．
解答： 解：（1）以D为原点DA、DC、DD1为x，y，z轴，建立坐标系．
设AE=x，则
DA1
=（1，0，1），
D1E
=（1，x，-1）．
∴
DA1
•
D1E
=0，
∴异面直线D1E与A1D所成角为
π
2
．   
（2）∵AD=AA1=1，AB=2，
∴CD1=
5
=AC，AD1=
2
，
过C做CF垂直AD1于F，则CF=
5-
2
4
=
3
2
2
，
∴S△ACD1=
1
2
×
2
×
3
2
2
=
3
2
，
设点E到平面ACD1的距离h，
则由VD1-AEC=VE-ACD1有
1
3
×
3
2
×h=
1
3
×
1
2
×1
得h=
1
3
．
点评：本题考查空间角的计算，考查点到面的距离，考查几何体体积的计算，属于中档题．
练习册系列答案
相关题目
如图，在正方体ABCD-A1B1C1D1中，E为线段A1C1的中点，则异面直线DE与B1C所成角的大小为（　　）
A、15°B、30°
C、45°D、60°
数列{an}、{bn}的每一项都是正数，a1=8，b1=16，且an、bn、an+1成等差数列，bn、an+1、bn+1成等比数列，n=1，2，3，…．
（Ⅰ）求a2、b2的值；
（Ⅱ）求数列{an}、{bn}的通项公式；
（Ⅲ）证明：对一切正整数n，有
1
a1-1
+
1
a2-1
+
1
a3-1
+…+
1
an-1
＜
2
7
．
若数列{An}满足An+1=An2，则称数列{An}为“平方递推数列”．已知数列{an}中，a1=9，点（an，an+1）在函数f（x）=x2+2x的图象上，其中n为正整数．
（Ⅰ）证明数列{an+1}是“平方递推数列”，且数列{lg（an+1）}为等比数列；
（Ⅱ）设（Ⅰ）中“平方递推数列”的前n项积为Tn，即Tn=（a1+1）（a2+1）…（an+1），求lgTn；
（Ⅲ）在（Ⅱ）的条件下，记bn=
lgTn
lg(an+1)
，求数列{bn}的前n项和Sn，并求使Sn＞4026的n的最小值．
已知非零数列{an}的递推公式为a1=1，an=an•an+1+2an+1（n∈N*）
（1）求证：数列{1+
1
an
}是等比数列；
（2）若关于n的不等式
1
n+log2(1+
1
a1
)
+
1
n+log2(1+
1
a2
)
+…+
1
n+log2(1+
1
an
)
＜m-
5
2
有解，求整数m的最小值．
（3）在数列{
1
an
+1-（-1）n}（1≤n≤11）中，是否一定存在首项、第r项、第s项（1＜r＜s≤11），使得这三项依次成等差数列？若存在，请指出r、s所满足的条件；若不存在，请说明理由．
已知函数f（x）=
1
x
+alnx．
（Ⅰ）若f（x）＞0恒成立，试求a的取值范围；
（Ⅱ）设h（x）=f（x）+ax-lnx，a∈[1，e]（e为自然对数的底），是否存在常数t，使h（x）≥t恒成立，若存在，求出t的取值范围；若不存在，请说明理由．
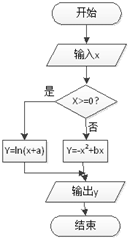小明在做一道函数题时，不小心将一个分段函数的解析式污染了一部分，但是已知这个函数的程序框图如图所示，且当分别输入数据-2，0 时，输出的结果都是0．
（Ⅰ）求这个分段函数的解析式并计算f（f（-1））；
（Ⅱ）若函数g（x）=f（x）-m有三个零点，求m的取值范围．
已知函数f（x）=ax3+bx2+cx+d（a≠0）的对称中心为M（x0，y0），记函数f（x）的导函数为f′（x），f′（x）的导函数为f″（x），则有f″（x0）=0．若函数f（x）=x3-3x2，则可求得f（
1
2013
）+f（
2
2013
）+…+f（
4024
2013
）+f（
4025
2013
）
 
．
设函数f（x）的定义域为D，如果存在正实数k，使对任意x∈D，都有x+k∈D，且f（x+k）＞f（x）恒成立，则称函数f（x）为D上的“k型增函数”．已知f（x）是定义在R上的奇函数，且当x＞0时，f（x）=|x-a|-2a，若f（x）为R上的“2014型增函数”，则实数a的取值范围是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网