题目内容

6．已知关于x的不等式$\frac{x+2}{x-a}≤2$的解集为P，若1∉P，则实数a的取值范围为（-$\frac{1}{2}$，1]．

分析 由题意知1不满足不等式，列出关于a的不等式，由分式不等式的解法求出实数a的取值范围．

解答 解：∵不等式$\frac{x+2}{x-a}≤2$的解集为p，且1∉P，
∴$\frac{1+2}{1-a}$＞2，即（a-1）（2a+1）＜0，
解得-$\frac{1}{2}$＜a＜1，
x=1时，不等式的解集为（1，6]，
∴实数a的取值范围是（-$\frac{1}{2}$，1]．
故答案为（-$\frac{1}{2}$，1]．

点评 本题考查了分式不等式的解法，以及转化思想，考查分析问题、解决问题的能力．

练习册系列答案
相关题目
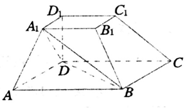14．如图所示，在四棱台ABCD-A1B1C1D1中，底面ABCD是平行四边形，DD1⊥平面ABCD，AB=2AD，AD=A1B1，∠BAD=60°．
（Ⅰ）证明：BD⊥平面ADD1A1；
（Ⅱ）证明：CC1∥平面A1BD；
（Ⅲ）若DD1=AD，求直线CC1与平面ADD1A1所成角的正弦值．
17．P为双曲线$C：\frac{x^2}{a^2}-\frac{y^2}{{{a^2}-4}}=1（a＞2）$上位于第一象限内一点，且$OP=2\sqrt{2}$，令∠POx=θ，则θ的取值范围是（0，$\frac{π}{12}$]．
14．对于定义在D上的函数f（x），点A（m，n）是f（x）图象的一个对称中心的充要条件是：对任意x∈D都有f（x）+f（2m-x）=2n，现给出下列三个函数：
（1）f（x）=x3+2x2+3x+4
（2）$f（x）=\frac{1}{x+1}+\frac{1}{x+2}+…+\frac{1}{x+2015}$
（3）$h（x）={log_2}\frac{x}{4-x}$
这三个函数中，图象存在对称中心的有（　　）
A．0个B．1个C．2个D．3个
1．定义区间（a，d），[a，d），（a，d]，[a，d]的长度为d-a（d＞a），已知a＞b，则满足$\frac{1}{x-a}+\frac{1}{x-b}≥1$的x构成的区间的长度之和为2．
11．已知$f（x）=\sqrt{{x^2}+x-2}$的定义域为$A\;，\;\;g（x）=\sqrt{\frac{2x+6}{3-x}}+{（{x+2}）^0}$的定义域为B，求A∩B．
18．某工厂生产甲、乙两种产品所得利润分别为P和Q（万元），它们与投入资金m（万元）的关系有经验公式P=$\frac{1}{3}$m+65，Q=76+4$\sqrt{m}$，今将150万元资金投入生产甲、乙两种产品，并要求对甲、乙两种产品的投资金额不低于25万元．
（1）设对乙产品投入资金x万元，求总利润y（万元）关于x的函数关系式及其定义域；
（2）如何分配使用资金，才能使所得总利润最大？最大利润为多少？
15．求函数y=lg（sin2x+2cosx+2）在$x∈[{-\frac{π}{6}\;，\;\;\frac{2π}{3}}]$上的最大值lg4，最小值lg$\frac{7}{4}$．
16．若偶函数f（x）在[0，+∞）上单调递减，设a=f（1），b=f（log0.53），c=f（log23-1），则（　　）
A．a＜b＜cB．b＜a＜cC．b＜c＜aD．c＜a＜b

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网