Question

1．定义区间（a，d），[a，d），（a，d]，[a，d]的长度为d-a（d＞a），已知a＞b，则满足$\frac{1}{x-a}+\frac{1}{x-b}≥1$的x构成的区间的长度之和为2．

Answer 1

分析 根据不等式进行化简，求出不等式对应的解集，根据区间长度的定义进行求解即可．

解答 解：∵$\frac{1}{x-a}+\frac{1}{x-b}≥1$，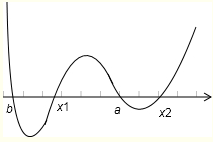
∴$\frac{2x-（a+b）}{（x-a）（x-b）}$≥1，
即$\frac{2x-（a+b）}{（x-a）（x-b）}$-1≥0，则$\frac{{x}^{2}-（2+a+b）x+ab+a+b}{（x-a）（x-b）}$≤0，
设x²-（2+a+b）x+ab+a+b=0的根为x₁和x₂．
则有求根公式得x₁=$\frac{a+b+2-\sqrt{（a-b）^{2}+4}}{2}$∈（a，b），
x₂=$\frac{a+b+2+\sqrt{（a-b）^{2}+4}}{2}$＞a，
x₁+x₂═2+a+b，
则由穿根法得不等式的解集为[b，x₁]∪[a-x₂]，
则构成的区间的长度之和x₁-b+x₂-a=x₁-x₂-a-b=2+a+b-a-b=2，
故答案为：2

点评 本题主要考查区间长度的定义，利用穿根法求出不等式的解集是解决本题的关键．