题目内容
10.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1,(a>0,b>0)$的左右焦点分别为F1,F2,过右焦点F2的直线交双曲线于A,B两点,连接AF1,BF1.若|AB|=|BF1|,且∠ABF1=90°,则双曲线的离心率为$\sqrt{5-2\sqrt{2}}$.分析 设|BF1|=n,由题意可得|AB|=n,|AF1|=$\sqrt{2}$n,运用双曲线的定义和勾股定理,化简整理,由离心率公式计算即可得到所求值.
解答 解:设|BF1|=n,由|AB|=|BF1|,且∠ABF1=90°,可得
|AB|=n,|AF1|=$\sqrt{2}$n,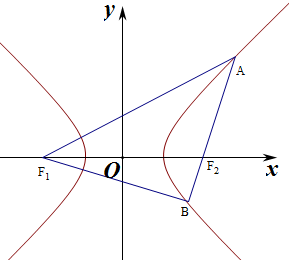
由双曲线的定义可得|BF1|-|BF2|=2a,
即有|BF2|=n-2a,
又|AF1|-|AF2|=2a,可得|AF2|=$\sqrt{2}$n-2a,
由|AB|=($\sqrt{2}$+1)n-4a=n,
解得n=2$\sqrt{2}$a,
在△F1F2B中,由|BF1|2+|BF2|2=|F1F2|2,
即为(2$\sqrt{2}$a)2+(2$\sqrt{2}$-2)2a2=4c2,
化为c2=(5-2$\sqrt{2}$)a2,
可得e=$\frac{c}{a}$=$\sqrt{5-2\sqrt{2}}$,
故答案为:$\sqrt{5-2\sqrt{2}}$,
点评 本题考查双曲线的离心率的求法,运用双曲线的定义和勾股定理是解决本题的关键,考查化简整理的运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知函数f(x)=x2(2x-2-x),则不等式f(2x+1)+f(1)<0的解集是( )
| A. | $({-∞,-\frac{1}{2}})$ | B. | (-∞,-1) | C. | $({-\frac{1}{2},+∞})$ | D. | (-1,+∞) |
18.若函数f(x)=sin(ωx-$\frac{π}{6}$)(ω>0)的图象相邻两个对称中心之间的距离为$\frac{π}{2}$,则f(x)的一个单调递增区间为( )
| A. | (-$\frac{π}{6}$,$\frac{π}{3}$) | B. | (-$\frac{π}{3}$,$\frac{π}{6}$) | C. | ($\frac{π}{6}$,$\frac{2π}{3}$) | D. | ($\frac{π}{3}$,$\frac{5π}{6}$) |
5.数学上称函数y=kx+b(k,b∈R,k≠0)为线性函数.对于非线性可导函数f(x),在点x0附近一点x的函数值f(x),可以用如下方法求其近似代替值:f(x)≈f(x0)+f'(x0)(x-x0).利用这一方法,$m=\sqrt{4.001}$的近似代替值( )
| A. | 大于m | B. | 小于m | ||
| C. | 等于m | D. | 与m的大小关系无法确定 |
15.若复数(a2-l)+(a-1)i(i为虚数单位)是纯虚数,则实数a=( )
| A. | ±1 | B. | -1 | C. | 0 | D. | 1 |
19.一家商场为了确定营销策略,进行了投入促销费用x和商场实际销售额y的试验,得到如下四组数据.
(1)求出x,y之间的回归直线方程$\widehaty$=$\widehatb$x+$\widehata$;
(2)若该商场计划营销额不低于600万元,则至少要投入多少万元的促销费用?
(注:$b=\frac{{\sum _{i=1}^n({{x_i}-\bar x})({{y_i}-\bar y})}}{{\sum _{i=1}^n{{({{x_i}-\bar x})}^2}}}=\frac{{\sum _{i=1}^n{x_i}{y_i}-n•\bar x•\bar y}}{{\sum _{i=1}^nx_i^2-n•{{\bar x}^2}}},a=\bar y-b•\bar x$)
| 投入促销费用x(万元) | 2 | 3 | 5 | 6 |
| 商场实际营销额y(万元) | 100 | 200 | 300 | 400 |
(2)若该商场计划营销额不低于600万元,则至少要投入多少万元的促销费用?
(注:$b=\frac{{\sum _{i=1}^n({{x_i}-\bar x})({{y_i}-\bar y})}}{{\sum _{i=1}^n{{({{x_i}-\bar x})}^2}}}=\frac{{\sum _{i=1}^n{x_i}{y_i}-n•\bar x•\bar y}}{{\sum _{i=1}^nx_i^2-n•{{\bar x}^2}}},a=\bar y-b•\bar x$)