题目内容
16.设两个非零向量$\vec a$与$\vec b$不共线.(1)若$\overrightarrow{AB}=\vec a+\vec b,\overrightarrow{BC}=2\vec a+8\vec b,\overrightarrow{CD}=3({\vec a-\vec b})$,求证:A,B,D三点共线
(2)试确定实数k,使$k\vec a+\vec b$和$\vec a+k\vec b$反向共线.
分析 (1)利用向量共线定理即可证明.
(2)利用向量共线定理即可证明.
解答 (1)证明:∵$\overrightarrow{AB}=\vec a+\vec b,\overrightarrow{BC}=2\vec a+8\vec b,\overrightarrow{CD}=3({\vec a-\vec b})$,
∴$\overrightarrow{BD}=\overrightarrow{BC}+\overrightarrow{CD}=2\vec a+8\vec b+3({\vec a-\vec b})$=$2\vec a+8\vec b+3\vec a-3\vec b=5({\vec a+\vec b})=5\overrightarrow{AB}$.
∴$\overrightarrow{AB},\overrightarrow{BD}$共线,又它们有公共点B,∴A,B,D三点共线.
(2)解:∵$k\vec a+\vec b$与$\vec a+k\vec b$反向共线,∴存在实数λ(λ<0),使$k\vec a+\vec b=λ({\vec a+k\vec b})$,
即$k\vec a+\vec b=λ\vec a+λk\vec b$,∴.$({k-λ})\vec a=({λk-1})\vec b$.
∵$\vec a,\vec b$是不共线的两个非零向量,∴k-λ=λk-1=0,
∴k2-1=0,∴k=±1,
∵λ<0,∴k=-1
点评 本题考查了向量共线定理,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.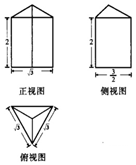 如图是由正三棱椎与正三棱柱组合而成的几何体的三视图,该几何体的顶点都在半径为R的球面上,则R=( )
如图是由正三棱椎与正三棱柱组合而成的几何体的三视图,该几何体的顶点都在半径为R的球面上,则R=( )
 如图是由正三棱椎与正三棱柱组合而成的几何体的三视图,该几何体的顶点都在半径为R的球面上,则R=( )
如图是由正三棱椎与正三棱柱组合而成的几何体的三视图,该几何体的顶点都在半径为R的球面上,则R=( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{1+\sqrt{2}}{2}$ | D. | $\sqrt{3}$ |
5.某学校课题组为了研究学生的数学成绩与学生细心程度的关系,在本校随机调查了100名学生进行研究.研究结果表明:在数学成绩及格的60名学生中有45人比较细心,另15人比较粗心;在数学成绩不及格的40名学生中有10人比较细心,另30人比较粗心.
(1)试根据上述数据完成2×2列联表;
(2)能否在犯错误的概率不超过0.001的前提下认为学生的数学成绩与细心程度有关系.
参考数据:独立检验随机变量K2的临界值参考表:
${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$(其中n=a+b+c+d)
(1)试根据上述数据完成2×2列联表;
| 数学成绩及格 | 数学成绩不及格 | 合计 | |
| 比较细心 | 45 | 10 | 55 |
| 比较粗心 | 15 | 30 | 45 |
| 合计 | 60 | 40 | 100 |
参考数据:独立检验随机变量K2的临界值参考表:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |