题目内容
5.数学上称函数y=kx+b(k,b∈R,k≠0)为线性函数.对于非线性可导函数f(x),在点x0附近一点x的函数值f(x),可以用如下方法求其近似代替值:f(x)≈f(x0)+f'(x0)(x-x0).利用这一方法,$m=\sqrt{4.001}$的近似代替值( )| A. | 大于m | B. | 小于m | ||
| C. | 等于m | D. | 与m的大小关系无法确定 |
分析 令f(x)=$\sqrt{x}$,根据定义计算近似值比较大小即可.
解答 解:根据题意,令f(x)=$\sqrt{x}$,则f′(x)=$\frac{1}{2\sqrt{x}}$>0,
取4.001附近的点x0=4,则有m的近似代替值为f(4)+$\frac{1}{2\sqrt{4}}$(4.001-4)=2+$\frac{0.001}{4}$,
∵(2+$\frac{0.001}{4}$)2=4+0.001+($\frac{0.001}{4}$)2>4.001=m2,
∴2+$\frac{0.001}{4}$>m.
故选A.
点评 本题考查导数的计算,关键是分析题意,理解“近似代替值”的意义.

练习册系列答案
相关题目
15.已知集合A={x|log2x>2},$B=\{x|{(\frac{1}{2})^x}≥\frac{1}{16}\}$,则下列结论成立的是( )
| A. | A∩B=A | B. | (∁RA)∩B=A | C. | A∩(∁RB)=A | D. | (∁RA)∩(∁RB)=A |
20.设全集U=R,集合M={x|x>1},p={x|x2>1},则下列关系中正确的是( )
| A. | M=P | B. | P?M | C. | M?P | D. | (∁UM)∩P=∅ |
17.一段长为36m的篱笆围成一个矩形菜园,求这个矩形菜园的最大面积( )
| A. | 79 | B. | 80 | C. | 81 | D. | 82 |
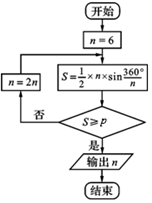 三世纪中期,魏晋时期的数学家刘徽首创割圆术,为计算圆周率建立了严密的理论和完善的算法,所谓割圆术,就是用圆内接正多边形的面积去无限逼近圆面积并以此求取圆周率的方法.按照这样的思路,刘徽把圆内接正多边形的面积一直算到了正3072边形,并由此而求得了圆周率为3.1415和 3.1416这两个近似数值.如图所示是利用刘徽的割圆术设计的程序框图,若输出的n=24,则p的值可以是(参考数据:$\sqrt{3}$=1.732,sin15°≈0.2588,sin7.5°≈0.1305,sin3.75°≈0.0654)( )
三世纪中期,魏晋时期的数学家刘徽首创割圆术,为计算圆周率建立了严密的理论和完善的算法,所谓割圆术,就是用圆内接正多边形的面积去无限逼近圆面积并以此求取圆周率的方法.按照这样的思路,刘徽把圆内接正多边形的面积一直算到了正3072边形,并由此而求得了圆周率为3.1415和 3.1416这两个近似数值.如图所示是利用刘徽的割圆术设计的程序框图,若输出的n=24,则p的值可以是(参考数据:$\sqrt{3}$=1.732,sin15°≈0.2588,sin7.5°≈0.1305,sin3.75°≈0.0654)( )