题目内容
下列命题中：
（1）
•
=0⇒
=
或
=
；
（2）
2•
2=(
•
)2；
（3）
=
；
（4）(
•
)
=
(
•
)对任意向量
，
，
都成立；
（5）对任意向量
，
，有（
+
）•（
-
）=（|
|+|
|）（|
|-|
|）．
写出其中所有正确命题的序号 ．
（1）
| a |
| b |
| a |
| 0 |
| b |
| 0 |
（2）
| a |
| b |
| a |
| b |
（3）
| ||||
|
| ||
|
（4）(
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
（5）对任意向量
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
写出其中所有正确命题的序号
考点：平面向量数量积的运算
专题：平面向量及应用
分析：根据平面向量的数量积运算性质，对每一个算式进行分析、判断，从而得出正确的结论．
解答：
解：对于（1），
•
=0时，
=
，或
=
，或
⊥
，∴（1）错误；
对于（2），
2•
2=|
|2•|
|2，(
•
)2=(|
|•|
|cos＜
，
＞)2，∴（2）错误；
对于（3），
=
=
，∴（3）错误；
对于（4），∵
•
、
•
是实数，∴(
•
)
=
(
•
)对任意向量
，
，
都成立是错误的；
对应（5），对任意向量
，
，有（
+
）•（
-
）=
2-
2=|
|2-|
|2，
（|
|+|
|）（|
|-|
|）=|
|2-|
|2，∴二者相等，（5）正确．
综上，正确的命题是（5）．
故答案为：（5）．
| a |
| b |
| a |
| 0 |
| b |
| 0 |
| a |
| b |
对于（2），
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
对于（3），
| ||||
|
|
| ||||||||
|
|
|
| ||||||
|
|
对于（4），∵
| a |
| b |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
对应（5），对任意向量
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
（|
| a |
| b |
| a |
| b |
| a |
| b |
综上，正确的命题是（5）．
故答案为：（5）．
点评：本题考查了平面向量的数量积的运算与性质的应用问题，解题时应对每一个算式进行分析，以便得出正确的结论，是基础题．
练习册系列答案
相关题目
已知函数f（x+1）的定义域为[1，2]，则函数y=f（
）的定义域为（ ）
| x+1 |
| A、[1，2] |
| B、[2，4] |
| C、[3，8] |
| D、[5，10] |
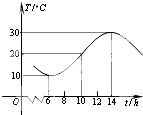如图，某地一天从6～14时的温度变化曲线近似满足函数y=Asin（ωx+φ）+b．