题目内容
设函数f(x)=
(其中|m|>1),区间M=[a,b](a<b),集合N={y|y=f(x),x∈M)},则使M=N成立的实对数(a,b)有 对.
| mx |
| 1+|x| |
考点:集合的相等
专题:函数的性质及应用,集合
分析:先判断函数f(x)是奇函数,进而从认知集合切入.这里的集合N为函数f(x),(x∈M)的值域.注意到f(x)的表达式中含有|x|,为求f(x)的值域,先将f(x)化为分段函数的形式,以便于化整为零,逐段分析.最后综合讨论结果,可得答案.
解答:
解:由函数f(x)=
(x∈R) 可得f(-x)=
=-
=-f(x),故函数f(x)是奇函数.
当x=0时,f(0)=0,
当x≠0时,f(x)=
,
当m<-1时,
若x>0,f(x)=
为减函数,若x>0,f(x)=
为减函数,
故函数f(x)在区间[a,b]上为减函数,
若M=N,则f(a)=b,且f(b)=a,
由点(a,b)与点(b,a)关于y=x对称,则a<0<b,
∴f(-a)=-f(a)=-b,
若b<-a,则f(b)>f(-a),a>-b,-a<b矛盾,
若b>-a,则f(b)<f(-a),a<-b,-a>b矛盾,
故b=-a,
x>0时,f(x)=-x,即
=-x,解得x=-1-m>0,
x<0时,f(x)=-x,即
=-x,解得x=1+m<0,
故M=[1+m,-1-m],
当m>1时,
若x>0,f(x)=
为增函数,若x>0,f(x)=
为增函数,
故函数f(x)在区间[a,b]上为增函数,
若M=N,则f(a)=a,且f(b)=b,
x>0时,f(x)=x,即
=x,解得x=-1+m,
x<0时,f(x)=x,即
=x,解得x=1-m,
x=0时,f(0)=0,
故M=[1-m,0],或M=[1-m,m-1],或M=[0,m-1]
综上所述,当m<-1时,使M=N成立的实对数(a,b)有1对,
当m>1时,使M=N成立的实对数(a,b)有3对.
故答案为:1或3
| mx |
| 1+|x| |
| -mx |
| 1+|-x| |
| mx |
| 1+|x| |
当x=0时,f(0)=0,
当x≠0时,f(x)=
| m | ||||
|
当m<-1时,
若x>0,f(x)=
| m | ||
1+
|
| m | ||
-1+
|
故函数f(x)在区间[a,b]上为减函数,
若M=N,则f(a)=b,且f(b)=a,
由点(a,b)与点(b,a)关于y=x对称,则a<0<b,
∴f(-a)=-f(a)=-b,
若b<-a,则f(b)>f(-a),a>-b,-a<b矛盾,
若b>-a,则f(b)<f(-a),a<-b,-a>b矛盾,
故b=-a,
x>0时,f(x)=-x,即
| m | ||
1+
|
x<0时,f(x)=-x,即
| m | ||
-1+
|
故M=[1+m,-1-m],
当m>1时,
若x>0,f(x)=
| m | ||
1+
|
| m | ||
-1+
|
故函数f(x)在区间[a,b]上为增函数,
若M=N,则f(a)=a,且f(b)=b,
x>0时,f(x)=x,即
| m | ||
1+
|
x<0时,f(x)=x,即
| m | ||
-1+
|
x=0时,f(0)=0,
故M=[1-m,0],或M=[1-m,m-1],或M=[0,m-1]
综上所述,当m<-1时,使M=N成立的实对数(a,b)有1对,
当m>1时,使M=N成立的实对数(a,b)有3对.
故答案为:1或3
点评:解决分段函数问题的基本策略:分段考察,综合结论.在这里,认知集合N仍是解题成败的关键所在.

练习册系列答案
相关题目

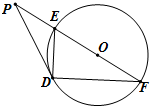 如图,P是圆O外一点,PD为切线,D为切点,割线PEF经过圆心O,若PF=12,PD=4
如图,P是圆O外一点,PD为切线,D为切点,割线PEF经过圆心O,若PF=12,PD=4