题目内容

函数y=2sin（ωx+
π
3
）的图象与直线y=-2的公共点中，相邻两点之间的距离为π，则正数ω=
 
．
考点：正弦函数的图象
专题：三角函数的图像与性质
分析：根据正弦函数的图象和性质，以及周期关系即可得到结论．
解答： 解：∵y=2sin（ωx+
π
3
）的图象与直线y=-2的公共点中，相邻两点之间的距离为π，
∴函数的周期为π，则T=
2π
ω
=π，
解得ω=2，
故答案为：2
点评：本题主要考查三角函数的图象和性质以及周期的求解和计算，比较基础．
练习册系列答案
相关题目
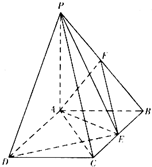如图，PA⊥平面ABCD，ABCD是矩形，PA=AB=
2
，AD=
3
，点F是PB的中点，点E是边BC上的动点．
（Ⅰ）求三棱锥E-PAD的体积；
（Ⅱ）当点E为BC的中点时，试判断EF与平面PAC的位置关系，并说明理由；
（Ⅲ）证明：无论点E在边BC的何处，都有PE⊥AF．
已知等差数列{an}的前项n和为Sn，且Sn=n-5an-85，n∈N*．
（1）证明：{an-1}是等比数列；
（2）求{Sn}的通项公式；
（3）求Sn取得最小值时n的值．
设a＞0为常数，条件p：|x-4|＞6；条件q：x2-2x+1-a2＞0，若p是q的充分不必要条件，求a的取值范围．
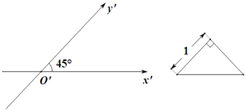已知一个三棱锥的高为3，其底面用斜二测画法所画出的水平放置的直观图是一个直角边长为1的等腰直角三角形（如右图所示），则此三棱锥的体积为（　　）
A、
2
B、6
2
C、
1
3
D、2
2
已知函数f（x）=2cosx（
3
sinx-cosx）+1（x∈R）
（1）求函数f（x）的最小正周期及在区间[0，
5π
12
]上的最大值和最小值；
（2）若f（x0）=
10
13
，x0∈[
π
2
，
7π
12
]，求cos2x0的值．
已知Sn为数列{an}的前n项和，Sn=
1
2
n2+
11
2
n；数列{bn}满足：b3=11，bn+2=2bn+1-bn，其前9项和为153．
（Ⅰ）求数列{an}、{bn}的通项公式；
（Ⅱ）设Tn为数列{cn}的前n项和，cn=
6
(2an-11)(2bn-1)
，求Tn．
若直线l1：x+（1+m）y=2-m与直线l2：2mx+4y=-16平行，则m=（　　）
A、m=-2
B、m=1
C、m=-2或 m=1
D、-
2
3
函数f（x）=21-|x|的图象是（　　）
A、
B、
C、
D、

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网