Question

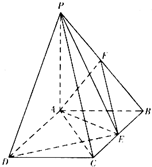如图，PA⊥平面ABCD，ABCD是矩形，PA=AB=

2

，AD=

3

，点F是PB的中点，点E是边BC上的动点．
（Ⅰ）求三棱锥E-PAD的体积；
（Ⅱ）当点E为BC的中点时，试判断EF与平面PAC的位置关系，并说明理由；
（Ⅲ）证明：无论点E在边BC的何处，都有PE⊥AF．

Answer 1

考点：棱柱、棱锥、棱台的体积,空间中直线与平面之间的位置关系,直线与平面垂直的性质

专题：计算题,证明题,空间位置关系与距离

分析：（Ⅰ）由于PA⊥平面ABCD，则V_E-PAD=V_P-ADE，运用棱锥的体积公式计算即得；
（Ⅱ）运用线面平行的判定定理，即可得证；
（Ⅲ）由线面垂直的性质和判定定理，即可得证．

解答： （Ⅰ）解：∵PA⊥平面ABCD，ABCD为矩形，
∴V_E-PAD=V_P-ADE，
=

1

3

×

1

2

×

3

×

2

×

2

=

3

3

；
（Ⅱ）EF与平面PAC平行．
理由如下：当E为BC中点时，∵F为PB的中点，
∴EF∥PC，
∵EF?平面PAC，PC?平面PAC，
∴EF∥平面PAC；
（Ⅲ）证明：∵PA=AB，F为PB的中点，
∴AF⊥PB，
∵PA⊥平面ABCD，∴PA⊥BC，
又BC⊥AB，BC⊥平面PAB，
又AF?平面PAB
∴BC⊥AF．
又PB∩BC=B，∴AF⊥平面PBC，
因无论点E在边BC的何处，都有PE?平面PBC，
∴PE⊥AF．

点评：本题考查直线与平面平行、垂直的判定和性质定理和运用，考查棱锥的体积公式，考查运算能力，属于中档题．