Question

已知圆：x²+y²-4x-6y+12=0，点P（x，y）为圆上任意一点，
（1）求

y

x

的最值；
（2）求（x+1）²+y²的最值．

Answer 1

考点：圆的一般方程

专题：直线与圆

分析：（1）设k=

y

x

，利用k的几何意义以及点到直线的距离公式即可进行求解；
（2）（x+1）²+y²的几何意义为P到定点A（-1，0）的距离的平方，利用圆的性质求出距离即可．

解答： 解：（1）圆的标准方程为（x-2）²+（y-3）²=1，
则圆心坐标为G（2，3），半径R=1，
设k=

y

x

，则y=kx，即kx-y=0，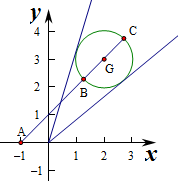
则满足圆心到直线的距离d=

|2k-3|

1+k2

≤1，
即|2k-3|≤

1+k2

，
平方得3k²-12k+8≤0，
解得

6-2 3

3

≤k≤

6+2 3

3

，
故

y

x

的最小值为

6-2 3

3

，最大值为

6+2 3

3

；
（2）（x+1）²+y²的几何意义为P到定点A（-1，0）的距离的平方．
则AG=

(-1-2)2+32

=

9+9

=3

2

，
P到定点A（-1，0）的最大距离为AC=3

2

+1，最小距离为AB=3

2

-1，
则（x+1）²+y²的最大值为（3

2

+1）²=19+6

2

，（x+1）²+y²的最小值（3

2

-1）²=19-6

2

．

点评：本题主要考查圆的方程的应用，利用斜率和距离的几何意义结合数形结合是解决本题的关键．