题目内容
函数f(x)=ln(x2+1)的值域是 .
考点:函数的值域
专题:计算题,函数的性质及应用
分析:这是一个求复合函数值域的问题,先求出内函数的取值范围,再求外函数即整个函数的值域.
解答:
解:令t=x2+1,则y=lnt,因为x2≥0,所以t≥1,所以y=lnt≥ln1=0,所以原函数的值域为[0,+∞).
故答案为:[0,+∞).
故答案为:[0,+∞).
点评:这是一道容易题,只要记住了函数y=lnx的单调性,并且会求二次函数的值域应该会做对.另外需强调的是,研究函数的性质一定要遵循定义域优先的原则,当然本题的定义域是R.

练习册系列答案
相关题目
已知数列{an}满足a1=2,an+1=
(n∈N*),则a2014=( )
| -1 |
| an+1 |
| A、2 | ||
B、-
| ||
C、-
| ||
D、
|
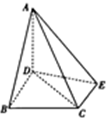 在三棱椎A-BCD中,AB=BC=4,AD=BD=CD=2
在三棱椎A-BCD中,AB=BC=4,AD=BD=CD=2