题目内容
已知直线y=
x-
与圆x2+y2=2相交于A,B两点,O为坐标原点,则△OAB的面积为 .
| 3 |
| 2 |
考点:直线与圆相交的性质
专题:直线与圆
分析:求出圆心到直线的距离,然后求出∠AOB,即可求解三角形的面积.
解答:
解:直线y=
x-
与圆x2+y2=2相交于A,B两点,O为坐标原点,
圆心到直线的距离为:d=
=
,
∵圆的半径为
,
∴∠AOB=120°,
∴△OAB的面积为S=
×
×
×sin120°=
.
故答案为:
.
| 3 |
| 2 |
圆心到直线的距离为:d=
|-
| ||||
|
| ||
| 2 |
∵圆的半径为
| 2 |
∴∠AOB=120°,
∴△OAB的面积为S=
| 1 |
| 2 |
| 2 |
| 2 |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查直线与圆的位置关系以及相交的性质,考查点到直线的距离公式以及三角形的面积的求法,考查计算能力.

练习册系列答案
相关题目
已知集合A={1,2,3},B={1,2,4},则A∩B等于( )
| A、{1,2,4} |
| B、{2,3,4} |
| C、{1,2} |
| D、{1,2,3,4} |
已知i是虚数单位,复数z=-i,则
的虚部为( )
| 1 |
| 1-z |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
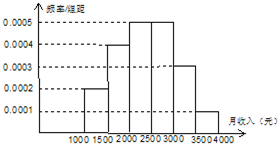 一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在[2500,3000)(元)/月收入段应抽出
一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在[2500,3000)(元)/月收入段应抽出