题目内容
已知数列{an}满足a1=2,an+1=
(n∈N*),则a2014=( )
| -1 |
| an+1 |
| A、2 | ||
B、-
| ||
C、-
| ||
D、
|
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:由数列的首项结合数列递推式依次求出a2,a3,a4,可知数列的项以3为周期周期出现,则答案可求.
解答:
解:由a1=2,an+1=
,得:
a2=
=-
,
a3=
=-
,
a4=
=2,
…
由上可知,数列{an}的项以3为周期周期出现,
∴a2014=a671×3+1=a1=2.
故选:A.
| -1 |
| an+1 |
a2=
| -1 |
| 2+1 |
| 1 |
| 3 |
a3=
| -1 | ||
-
|
| 3 |
| 2 |
a4=
| -1 | ||
-
|
…
由上可知,数列{an}的项以3为周期周期出现,
∴a2014=a671×3+1=a1=2.
故选:A.
点评:本题考查了数列递推式,考查了数列的函数特性,解答的关键是分析出数列的周期,是中档题.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
从1,2,3,…,10这10个数中选出互不相邻的3个数的方法种数是( )
| A、56 | B、57 | C、58 | D、60 |
设p:x=3,q:x2-2x-3=0,则下面表述正确的是( )
| A、p是q的充分条件,但p不是q的必要条件 |
| B、p是q的必要条件,但p不是q的充分条件 |
| C、p是q的充要条件 |
| D、p既不是q的充分条件也不是q的必要条件 |
若(x2-
)9(a∈R)的展开式中x9项的系数为-
,则函数f(x)=sinx与直线x=a、x=-a及x轴围成的封闭图形的面积为( )
| 1 |
| ax |
| 21 |
| 2 |
| A、2-2cos2 |
| B、4-2cos1 |
| C、0 |
| D、2+2cos2 |
已知i是虚数单位,复数z=-i,则
的虚部为( )
| 1 |
| 1-z |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
“p∧q是假命题”是“¬p为真命题”的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
若函数f(x)=sin(2x+φ)满足f(x)≥f(
),则函数f(x)的单调递增区间是( )
| π |
| 3 |
A、[2kπ-
| ||||
B、[2kπ+
| ||||
C、[kπ-
| ||||
D、[kπ+
|
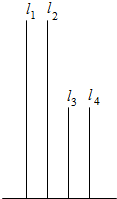
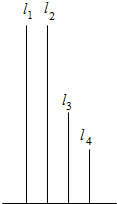
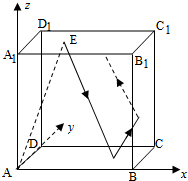 如图,在长方体ABCD-A1B1C1D1中,AB=11,AD=7,AA1=12.一质点从顶点A射向点E(4,3,12),遇长方体的面反射(反射服从光的反射原理),将第i-1次到第i次反射点之间的线段记为li(i=2,3,4),l1=AE,将线段l1,l2,l3,l4竖直放置在同一水平线上,则大致的图形是( )
如图,在长方体ABCD-A1B1C1D1中,AB=11,AD=7,AA1=12.一质点从顶点A射向点E(4,3,12),遇长方体的面反射(反射服从光的反射原理),将第i-1次到第i次反射点之间的线段记为li(i=2,3,4),l1=AE,将线段l1,l2,l3,l4竖直放置在同一水平线上,则大致的图形是( )