题目内容
已知四边形ABCD是正方形，BE∥AC，AC=CE，EC的延长线交BA的延长线于F，求证：AF=AE．
考点：向量在几何中的应用
专题：平面向量及应用
分析：可以以A为原点建立平面直角坐标系，然后据题意给出点A，B，C，D的坐标，然后根据BE∥AC，AC=CE，利用待定系数法求出E点的坐标，然后可得CE的直线方程，则F的坐标可求，问题即可解决．
解答：
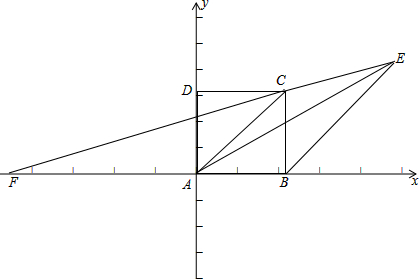证明：如图所示，以A为原点建立平面直角坐标系，不妨设正方形边长为2，则A（0，0），B（2，0），C（2，2），D（0，2）．
再设E（x，y），由BE∥AC，AC=CE得：
∥
，结合
=(2，2)，
=(x-2，y)．
所以
，解得
或
．
当E（3+
，1+
）时，易求得直线CE方程为y-2=(2-
)(x-2)．
令y=0得xF=-2(
+1)，故AF=2(
+1)．
此时AE=
=2(
+1)．所以AF=AE．
当E（3-
，1-
）时，易求得CE方程为y-2=(2+
)(x-2)．
令y=0得xF=2(
-1)．所以AF=2(
-1)，又AE=
=2(
-1)．
综上，AE=AF成立．
证明：如图所示，以A为原点建立平面直角坐标系，不妨设正方形边长为2，则A（0，0），B（2，0），C（2，2），D（0，2）．再设E（x，y），由BE∥AC，AC=CE得：
| AC |
| BE |
| AC |
| BE |
所以
|
|
|
当E（3+
| 3 |
| 3 |
| 3 |
令y=0得xF=-2(
| 3 |
| 3 |
此时AE=
(3+
|
| 3 |
当E（3-
| 3 |
| 3 |
| 3 |
令y=0得xF=2(
| 3 |
| 3 |
(3-
|
| 3 |
综上，AE=AF成立．
点评：本题考查了利用向量法证明几何问题的基本思路，一般先建系，然后设点，再利用题目给的共线、垂直、距离、角度等条件列出方程求解即可．
练习册系列答案
相关题目