题目内容
已知函数f（x）=
，其中a为实常数．
（1）若该函数为奇函数，求实数a的值．
（2）当a=-1时，求该函数的值域并讨论该函数的单调性，说明理由．
| a•5x+(a-2)•5-x |
| 5x+5-x |
（1）若该函数为奇函数，求实数a的值．
（2）当a=-1时，求该函数的值域并讨论该函数的单调性，说明理由．
考点：函数奇偶性的判断,函数单调性的判断与证明
专题：函数的性质及应用
分析：（1）利用奇函数定义域为R，则f（0）=0，求得a．
（2）当a=-1时，代入解析式得到f（x），理由幂函数的单调性求其值域．
（2）当a=-1时，代入解析式得到f（x），理由幂函数的单调性求其值域．
解答：
解：（1）因为该函数为奇函数，并且定义域为R，所以（0）=0，即
=0，解得a=1；
（2）当a=-1时，该函数为f（x）=
=
=
=-1-
，值域为（-2，-1）；
理由如下：
因为25x＞0，所以25x+1＞1，-1＜
＜0，-2＜-1-
＜-1，
所以它的值域为（-2，-1）．
| a+a-2 |
| 2 |
（2）当a=-1时，该函数为f（x）=
| -5x-3×5-x |
| 5x+5-x |
-5x-
| ||
5x+
|
| -25x-3 |
| 25x+1 |
| 2 |
| 25x+1 |
理由如下：
因为25x＞0，所以25x+1＞1，-1＜
| -2 |
| 25x+1 |
| 2 |
| 25x+1 |
所以它的值域为（-2，-1）．
点评：本题考查函数的奇偶性的运用、值域的求法，本题利用了奇函数在x=0处的函数值为0求a，属基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知log7（2
-1）+log2（
+1）=a，则log7（2
+1）+log2（
-1）=（ ）
| 2 |
| 2 |
| 2 |
| 2 |
| A、1+a | B、1-a | C、a | D、-a |
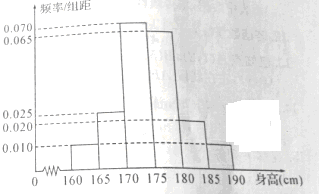为了调查某校高三男生的身高和相关的运动指标，在该校高三男学生中随机抽取了若干名同学作为样本，测得他们的身高后，画出频率分布直方图如图所示，若185～190身高段的人数为2人．