题目内容
在直角坐标系中,把双曲线C1:
-y2=1绕原点逆时针旋转90°得到双曲线C2,给出下列说法:
①C1与C2的离心率相同;②C1与C2的焦点坐标相同;③C1与C2的渐近线方程相同;④C1与C2的实轴长相等.
其中正确的说法有( )
| x2 |
| 2 |
①C1与C2的离心率相同;②C1与C2的焦点坐标相同;③C1与C2的渐近线方程相同;④C1与C2的实轴长相等.
其中正确的说法有( )
| A、①② | B、②③ | C、①④ | D、③④ |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:把双曲线C1:
-y2=1绕原点逆时针旋转90°后,只需将原方程中x,y互换即可得到C2:
-x2=1.
对于①,由a,b的值,可知离心率改变与否;
对于②,由于双曲线的位置改变,可知焦点位置改变;
对于③,在C2:
-x2=1中,令
-x2=0,即得渐近线方程;
对于④,由于双曲线的形状未变,可知实轴长未变.
| x2 |
| 2 |
| y2 |
| 2 |
对于①,由a,b的值,可知离心率改变与否;
对于②,由于双曲线的位置改变,可知焦点位置改变;
对于③,在C2:
| y2 |
| 2 |
| y2 |
| 2 |
对于④,由于双曲线的形状未变,可知实轴长未变.
解答:
解:旋转后,双曲线C2的实轴在y轴上,焦点也在y轴上,
其方程为
-x2=1,a=
,b=1,c=
=
=
,
考虑①、④:因为a,b,c未变,所以离心率e=
不变,实轴长2a不变.
考虑②:因为焦点的位置改变,所以C1与C2的焦点坐标不同.
考虑③:在C2的方程
-x2=1中,令
-x2=0,得渐近线方程为y=±
x,
在C1:
-y2=1中,令
-y2=0,得渐近线方程为y=±
x,
所以渐近线方程不同.
所以正确的选项是①④.
故选C.
其方程为
| y2 |
| 2 |
| 2 |
| a2+b2 |
| 2+1 |
| 3 |
考虑①、④:因为a,b,c未变,所以离心率e=
| c |
| a |
考虑②:因为焦点的位置改变,所以C1与C2的焦点坐标不同.
考虑③:在C2的方程
| y2 |
| 2 |
| y2 |
| 2 |
| 2 |
在C1:
| x2 |
| 2 |
| x2 |
| 2 |
| ||
| 2 |
所以渐近线方程不同.
所以正确的选项是①④.
故选C.
点评:本题考查了双曲线的方程及双曲线的焦点、离心率、实轴、渐近线等几何性质,关键是知道双曲线的方程与双曲线的焦点、离心率、实轴、渐近线的关系.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
将3张不同的奥运门票分给10名同学中的3人,每人1张,则不同的分法有( )
| A、2610种 | B、720种 |
| C、240种 | D、60种 |
下列函数中,在其定义域上为奇函数的是( )
| A、y=ex+e-x | ||
B、y=-
| ||
| C、y=tan|x| | ||
D、y=ln
|
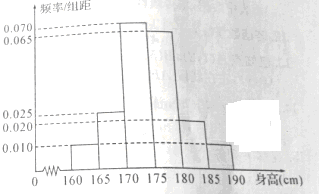 为了调查某校高三男生的身高和相关的运动指标,在该校高三男学生中随机抽取了若干名同学作为样本,测得他们的身高后,画出频率分布直方图如图所示,若185~190身高段的人数为2人.
为了调查某校高三男生的身高和相关的运动指标,在该校高三男学生中随机抽取了若干名同学作为样本,测得他们的身高后,画出频率分布直方图如图所示,若185~190身高段的人数为2人.