题目内容
1.f(x)=x2+ax+b与坐标轴有三个交点A,B,C,且△ABC外心在y=x上,则a+b=( )| A. | 1 | B. | -1 | C. | 0 | D. | -2 |
分析 可画出图形,设得到C(0,b),然后设A(x1,0),B(x2,0),且x1<x2,设O1为△ABC的外心,从而可得到${x}_{1}=\frac{-a-\sqrt{{a}^{2}-4b}}{2},{x}_{1}+{x}_{2}=-a$,这样根据O1在y=x便可得到${O}_{1}(-\frac{a}{2},-\frac{a}{2})$,从而由|O1A|=|O1C|便可以得到b(a+b+1)=0,而容易说明b≠0,从而有a+b+1=0,这便得出a+b的值.
解答 解:如图,易得C(0,b),设A(x1,0),B(x2,0),x1<x2,O1为△ABC的外心,则: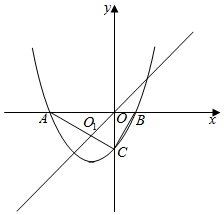
x1,x2为方程x2+ax+b=0的两个实根;
∴${x}_{1}=\frac{-a-\sqrt{{a}^{2}-4b}}{2},{x}_{1}+{x}_{2}=-a$;
∴O1的横坐标为$-\frac{a}{2}$,又O1在y=x上;
∴${O}_{1}(-\frac{a}{2},-\frac{a}{2})$;
由|O1A|=|O1C|得,$(-\frac{a}{2}-\frac{-a-\sqrt{{a}^{2}-4b}}{2})^{2}+(-\frac{a}{2}-0)^{2}$=$(-\frac{a}{2}-0)^{2}+(-\frac{a}{2}-b)^{2}$;
整理得,ab+b2+b=0;
∴b(a+b+1)=0;
显然b≠0,否则f(x)的图象与坐标轴只有2个交点;
∴a+b+1=0;
∴a+b=-1.
故选:B.
点评 考查二次函数f(x)图象和x轴交点的坐标与方程f(x)=0实根的关系,一元二次方程的求根公式,以及韦达定理,三角形外心的概念,两点间的距离公式.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
11.若全集U={0,1,2,4},且∁UA={1,2},则集合A=( )
| A. | {1,4} | B. | {0,4} | C. | {2,4} | D. | {0,2} |
12.复数z1,z2在复平面内对应的点关于直线y=x对称,且z1=3+2i,则z2=( )
| A. | 3-2i | B. | 2-3i | C. | -3-2i | D. | 2+3i |
16.在正方体ABCD-A1B1C1D1中,E为棱AA1的中点,F是棱A1B1上的点,且A1F:FB1=1:3,则异面直线EF与BC1所成角的正弦值为( )
| A. | $\frac{{\sqrt{15}}}{3}$ | B. | $\frac{{\sqrt{15}}}{5}$ | C. | $\frac{{\sqrt{5}}}{3}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
6.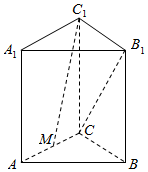 如图,在直三棱柱ABC-A1B1C1中,AB=BC=CC1=2,AC=2$\sqrt{3}$,M是AC的中点,则异面直线CB1与C1M所成角的余弦值为$\frac{\sqrt{14}}{28}$.
如图,在直三棱柱ABC-A1B1C1中,AB=BC=CC1=2,AC=2$\sqrt{3}$,M是AC的中点,则异面直线CB1与C1M所成角的余弦值为$\frac{\sqrt{14}}{28}$.
 如图,在直三棱柱ABC-A1B1C1中,AB=BC=CC1=2,AC=2$\sqrt{3}$,M是AC的中点,则异面直线CB1与C1M所成角的余弦值为$\frac{\sqrt{14}}{28}$.
如图,在直三棱柱ABC-A1B1C1中,AB=BC=CC1=2,AC=2$\sqrt{3}$,M是AC的中点,则异面直线CB1与C1M所成角的余弦值为$\frac{\sqrt{14}}{28}$.
13.已知圆O:x2+y2=9;直线l过点(0,3),倾斜角为α,α在区(0,π)内随机取值,l与圆O相交于A、B两点,则|AB|≤3$\sqrt{2}$的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
10.已知正方体ABCD-A1B1C1D1,其棱长为2,P为该正方体内随机一点,则满足|PA|≤1的概率是( )
| A. | $\frac{π}{48}$ | B. | $\frac{π}{24}$ | C. | $\frac{π}{12}$ | D. | $\frac{1}{8}$ |