题目内容
12.点P在抛物线x2=4y上,F为抛物线焦点,|PF|=5,以P为圆心|PF|为半径的圆交x轴于A,B两点,则$\overrightarrow{AP}$•$\overrightarrow{AB}$=( )| A. | 9 | B. | 12 | C. | 18 | D. | 32 |
分析 利用抛物线的焦半径公式,求得P点坐标,即可求得圆P,当y=0,即可求得A和B坐标,根据向量数量积的坐标运算,即可求得答案.
解答 解:抛物线x2=4y的焦点F(0,1),设P(x,y),由抛物线的焦半径公式丨PF丨=y+$\frac{p}{2}$,即y+1=5,则y=4,x=±4,
假设P(4,4),则圆的方程为(x-4)2+(y-4)2=25,
令y=0,解得:x=1或x=7,则A(1,0),B(7,0),
则$\overrightarrow{AP}$=(3,4),$\overrightarrow{AB}$=(6,0),$\overrightarrow{AP}$•$\overrightarrow{AB}$=3×6+4×0=18,
故选:C.
点评 本题考查抛物线的焦半径公式,考查圆的方程,向量数量积的坐标运算,考查计算能力,属于中档题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
7.若$cos2α=\frac{7}{25}$,α是第三象限的角,则$sin(α-\frac{π}{4})$=( )
| A. | $-\frac{{7\sqrt{2}}}{10}$ | B. | $-\frac{{\sqrt{2}}}{10}$ | C. | $\frac{{7\sqrt{2}}}{10}$ | D. | $\frac{{\sqrt{2}}}{10}$ |
1.若直线x+y-2=0与直线x-y=0的交点P在角α的终边上,则tanα的值为( )
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | $\sqrt{5}$ |

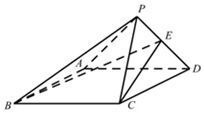 如图,四棱锥P-ABCD中,底面ABCD边长为4的正方形,PA=PD=2$\sqrt{2}$,平面PAD⊥平面PCD;
如图,四棱锥P-ABCD中,底面ABCD边长为4的正方形,PA=PD=2$\sqrt{2}$,平面PAD⊥平面PCD;