题目内容
已知f(x)=
是R上的单调增函数,则实数a的取值范围为 .
|
|
考点:函数单调性的性质
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:运用指数函数和一次函数的单调性,结合R上的单调增函数,可得a>1且4-
>0且a≥4-
+2,分别解出它们,再求交集即可.
| a |
| 2 |
| a |
| 2 |
解答:
解:由f(x)是R上的单调增函数,
则当x>1时,由指数函数的单调性可得a>1,
当x≤1时,由一次函数的单调性可得4-
>0,
可得a<8,
再由R上递增,则a≥4-
+2,
解得a≥4,
综上可得,4≤a<8.
故答案为:[4,8).
则当x>1时,由指数函数的单调性可得a>1,
当x≤1时,由一次函数的单调性可得4-
| a |
| 2 |
可得a<8,
再由R上递增,则a≥4-
| a |
| 2 |
解得a≥4,
综上可得,4≤a<8.
故答案为:[4,8).
点评:本题考查函数的单调性的运用:求参数范围,考查指数函数和一次函数的单调性,考查运算能力,属于中档题和易错题.

练习册系列答案
相关题目
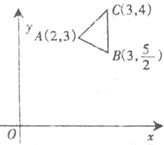 已知点(x,y)在△ABC所包围的区域内(包含边界),若B(3,
已知点(x,y)在△ABC所包围的区域内(包含边界),若B(3,| 5 |
| 2 |
A、a≥-
| ||
| B、a>0 | ||
C、a≤-
| ||
D、-
|
方程(x-y-3)(x+y)=0所表示的图形是( )
| A、两条互相平行的直线 | ||||
| B、两条互相垂直的直线 | ||||
C、一个点(
| ||||
D、过点(
|