题目内容
已知函数f（x）=
，证明函数f（x）在（-∞，0）上是减函数．
| x+1 |
| x |
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：先化简函数f（x），再用定义证明f（x）在（-∞，0）上是减函数即可．
解答：
解：∵函数f（x）=
=1+
，
现证明函数f（x）在（-∞，0）上是减函数；
任取x1、x2∈（-∞，0），且x1＜x2，
则f（x1）-f（x2）=（1+
）-（1+
）
=
，
∵x1x2＞0，x2-x1＞0，
∴f（x1）-f（x2）＞0，
∴f（x1）＞f（x2），
∴f（x）在（-∞，0）上是减函数．
| x+1 |
| x |
| 1 |
| x |
现证明函数f（x）在（-∞，0）上是减函数；
任取x1、x2∈（-∞，0），且x1＜x2，
则f（x1）-f（x2）=（1+
| 1 |
| x1 |
| 1 |
| x2 |
=
| x2-x1 |
| x1x2 |
∵x1x2＞0，x2-x1＞0，
∴f（x1）-f（x2）＞0，
∴f（x1）＞f（x2），
∴f（x）在（-∞，0）上是减函数．
点评：本题考查了用单调性的定义证明函数的单调性问题，是基础题目．
练习册系列答案
阅读快车系列答案
相关题目
若复数z满足（1-3i）z=10i，则z等于（ ）
| A、-1-3i | B、3-i |
| C、1+3i | D、-3+i |
下列各式正确的是（ ）
A、0•
| ||||
B、0•
| ||||
C、0•a=
| ||||
D、
|
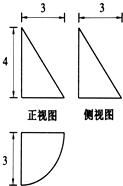某几何体的三视图（单位：cm）如图所示，其中俯视图中的曲线是四分之一的圆弧，则该几何体的体积等于