题目内容
利用“五点法”换函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<
)的图象时,先列表(部分数据)如下:
(1)根据表格提供的份额数据求函数f(x)的解析式以及单调递增区间;
(2)若当x∈[0,
]时,方程f(x)=m+1恰有两个不同的解,求实数m的取值范围,并求这两个解的和.
| π |
| 2 |
| ωx+φ | 0 | π | 2π | ||||||||||||
| x |
|
|
|
|
| ||||||||||
| y | 4 | -2 |
(2)若当x∈[0,
| 7π |
| 6 |
考点:五点法作函数y=Asin(ωx+φ)的图象
专题:三角函数的图像与性质
分析:(1)由最值求出A、B的值,由周期求出ω,由特殊点的坐标求出φ的值,可得函数的解析式.
(2)将方程f(x)=m+1进行转化,利用正弦函数的定义域和值域求得实数m的取值范围.
(2)将方程f(x)=m+1进行转化,利用正弦函数的定义域和值域求得实数m的取值范围.
解答:
解:(1)由题意可知
,解得ω=1,φ=-
,
由
,解得A=3,B=1,即f(x)=3sin(x-
)+1,
由2kπ-
≤x-
≤2kπ+
,k∈Z,
得2kπ-
≤x≤2kπ+
,k∈Z,
则函数f(x)的单调递增区间是[2kπ-
,2kπ+
],k∈Z;
(2)由f(x)=3sin(x-
)+1=m+1得m=3sin(x-
),
∵x∈[0,
],
∴x-
∈[-
,
],
由正弦函数的图象可知,要使方程f(x)=m+1恰有两个不同的解,
则实数m的取值范围是[
,3),
设这两个实数解为x1,x2,
则(x1-
)+(x2-
)=2×
,
即x1+x2=
.
|
| π |
| 3 |
由
|
| π |
| 3 |
由2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
得2kπ-
| π |
| 6 |
| 5π |
| 6 |
则函数f(x)的单调递增区间是[2kπ-
| π |
| 6 |
| 5π |
| 6 |
(2)由f(x)=3sin(x-
| π |
| 3 |
| π |
| 3 |
∵x∈[0,
| 7π |
| 6 |
∴x-
| π |
| 3 |
| π |
| 3 |
| 5π |
| 6 |
由正弦函数的图象可知,要使方程f(x)=m+1恰有两个不同的解,
则实数m的取值范围是[
| 3 |
| 2 |
设这两个实数解为x1,x2,
则(x1-
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
即x1+x2=
| 5π |
| 3 |
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由周期求出ω,由特殊点的坐标求出φ的值,正弦函数的单调性、对称性、定义域和值域,综合考查三角函数的图象和性质.

练习册系列答案
相关题目
经过点A(-4,3)且与原点的距离等于5的直线方程是( )
| A、3x-4y+25=0 |
| B、4x-3y-25=0 |
| C、4x-3y+25=0 |
| D、4x+3y+25=0 |
已知集合M={x|2x>1},若a∉M,则实数a可以是( )
| A、3 | B、2 | C、1 | D、-1 |
函数y=
的定义域为R,则实数k的取值范围为( )
| x |
| kx2+kx+1 |
| A、k<0或k>4 |
| B、k≥4或k≤0 |
| C、0≤k<4 |
| D、0<k<4 |
在一块并排10垄的土地上,选择2垄分别种植A、B两种植物,每种植物种植一垄.为有利于植物生长,要求A、B两种植物的间隔不小于6垄的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
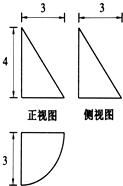 某几何体的三视图(单位:cm)如图所示,其中俯视图中的曲线是四分之一的圆弧,则该几何体的体积等于
某几何体的三视图(单位:cm)如图所示,其中俯视图中的曲线是四分之一的圆弧,则该几何体的体积等于