题目内容
已知函数f(x)的图象如图所示,若函数y=f(x)-
-a在区间[-10,10]上有10个零点(互不相同),则实数a的取值范围是( )

| 1 |
| x |

A、[-
| ||||
B、(-
| ||||
C、[-
| ||||
D、(-
|
考点:函数零点的判定定理
专题:函数的性质及应用
分析:可采用数形结合的方法解决问题,因为f(x)-
是奇函数,只需判断a≥0时的满足题意的a的范围,然后即可解决问题.
| 1 |
| x |
解答:
解:y=f(x)-
-a在区间[-10,10]上有10个零点(互不相同),即函数y=f(x)与y=g(x)=
+a的图象在[-10,10]上有10个不同的交点.
先研究a≥0时的情况,如图,当a=0时,g(x)=
恰好与y=f(x)产生10个交点;
当a>0时,y=
+a的图象是将y=
向上平移a个单位,则在y轴右边,当g(9)<1时,右边产生4个交点;
同时y轴左边满足g(-10)≤0时,左边产生6个交点.
这样共产生10个交点,即
,解得0≤a≤
.
同理,根据函数图象的对称性可知,当a<0时,只需-
≤a<0时满足题意.
综上,当-
≤a≤
时,
函数y=f(x)-
-a在区间[-10,10]上有10个零点(互不相同).

故选C
| 1 |
| x |
| 1 |
| x |
先研究a≥0时的情况,如图,当a=0时,g(x)=
| 1 |
| x |
当a>0时,y=
| 1 |
| x |
| 1 |
| x |
同时y轴左边满足g(-10)≤0时,左边产生6个交点.
这样共产生10个交点,即
|
| 1 |
| 10 |
同理,根据函数图象的对称性可知,当a<0时,只需-
| 1 |
| 10 |
综上,当-
| 1 |
| 10 |
| 1 |
| 10 |
函数y=f(x)-
| 1 |
| x |

故选C
点评:本题考查了数形结合的方法研究函数的零点个数的问题,要注意参数变化时函数图象的变化规律.属于中档题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
S=1+(1+2)+(1+2+22)+…+(1+2+22+…+210)的值是( )
| A、211-11 |
| B、211-13 |
| C、212-13 |
| D、213-11 |
过点M(0,1)与抛物线y2=2x只有一个公共点的直线有( )
| A、1条 | B、2条 | C、3条 | D、0条 |
定义f(x)•g(x)=
,函数F(x)=(x2-1)•(x)-k的图象与x轴有两个不同的交点,则实数k的取值范围是 ( )
|
| A、k≥3或0≤k<1 |
| B、k>3或0<k<1 |
| C、k≤1或k≥3 |
| D、0≤k≤1或k>3 |
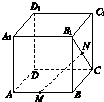 如图,在正方体ABCD-A1B1C1D1中,M、N分别为AB、B1C的中点,设
如图,在正方体ABCD-A1B1C1D1中,M、N分别为AB、B1C的中点,设| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| MN |
| a |
| b |
| c |
A、x=
| ||||||
B、x=
| ||||||
C、x=
| ||||||
D、x=
|
不等式(x-1)(x-2)(x-3)>0的解集是( )
| A、(1,2) |
| B、(1,2)∪(3,+∞) |
| C、(1,3) |
| D、(2,3) |
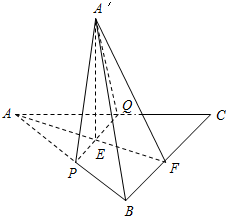 如图所示,等边△ABC的边长为a,将它沿平行于BC的线段PQ折起,使平面A′PQ⊥平面BPQC,若折叠后A′B的长为d,则d的最小值为
如图所示,等边△ABC的边长为a,将它沿平行于BC的线段PQ折起,使平面A′PQ⊥平面BPQC,若折叠后A′B的长为d,则d的最小值为