题目内容
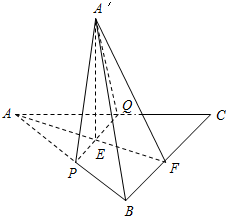 如图所示,等边△ABC的边长为a,将它沿平行于BC的线段PQ折起,使平面A′PQ⊥平面BPQC,若折叠后A′B的长为d,则d的最小值为
如图所示,等边△ABC的边长为a,将它沿平行于BC的线段PQ折起,使平面A′PQ⊥平面BPQC,若折叠后A′B的长为d,则d的最小值为考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:取BC中点为F,折叠后A′BF为一直角三角形,A′F的长度最短时,A′B长度取到最小值,由此能求出d的最小值.
解答:
 解:取BC中点为F,折叠后A′BF为一直角三角形,
解:取BC中点为F,折叠后A′BF为一直角三角形,
且∠A′FB=90°,由于BF在折叠前后长度不变,
由勾股定理可以得到,折叠后A′B2=B′F2+A′F2,
所以A′F的长度最短时,A′B长度取到最小值,
设AF与PQ交于E,
设AE长度为x,在直角△A′EF中,A′E2+EF2=A′F2 ,
∴A′F2 =x2+(
-x)2
=2(x-
)2+
a2,
∴x=
时,A′F取到最小值
=
a.
∴dmin=
=
a.
故答案为:
a.
 解:取BC中点为F,折叠后A′BF为一直角三角形,
解:取BC中点为F,折叠后A′BF为一直角三角形,且∠A′FB=90°,由于BF在折叠前后长度不变,
由勾股定理可以得到,折叠后A′B2=B′F2+A′F2,
所以A′F的长度最短时,A′B长度取到最小值,
设AF与PQ交于E,
设AE长度为x,在直角△A′EF中,A′E2+EF2=A′F2 ,
∴A′F2 =x2+(
| ||
| 2 |
=2(x-
| ||
| 4 |
| 3 |
| 8 |
∴x=
| ||
| 4 |
|
| ||
| 4 |
∴dmin=
(
|
| ||
| 4 |
故答案为:
| ||
| 4 |
点评:本题考查线段的长度的最小值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
已知函数f(x)的图象如图所示,若函数y=f(x)-
-a在区间[-10,10]上有10个零点(互不相同),则实数a的取值范围是( )

| 1 |
| x |

A、[-
| ||||
B、(-
| ||||
C、[-
| ||||
D、(-
|
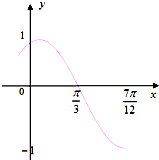 函数f(x)=sin(ωx+φ)的图象如图所示,其中ω>0,|φ|<
函数f(x)=sin(ωx+φ)的图象如图所示,其中ω>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|