题目内容
已知函数f(x)=x2-2x+a,其中a>0,若存在实数t,使f(t)<0,则f(t+2)•f(
)的值为 .
| 2t+1 |
| 3 |
考点:二次函数的性质
专题:函数的性质及应用
分析:由已知可得f(x)=x2-2x+a<0的解集(m,n),满足(m,n)⊆(0,2),进而分析f(t)<0时,f(t+2),f(
)的符号,进而可得f(t+2)•f(
)的符号.
| 2t+1 |
| 3 |
| 2t+1 |
| 3 |
解答:
解:∵f(x)=x2-2x+a=0,
则|x2-x1|2=(x2+x1)2-4x2•x1=4-4a,
∵0<4-4a<4,
∴0<|x2-x1|<2,
又∵f(0)=f(2)=a>0,函数f(x)图象的对称轴x=1∈(0,2),
设f(x)=x2-2x+a<0的解集为(m,n),
则(m,n)⊆(0,2),
当t∈(m,n)⊆(0,2)时,
t+2∈(2,4),故f(t+2)>0,
∈(
,
)⊆(m,n),故f(
)<0,
故f(t+2)•f(
)<0,
即f(t+2)•f(
)的值为负.
故答案为:负.
则|x2-x1|2=(x2+x1)2-4x2•x1=4-4a,
∵0<4-4a<4,
∴0<|x2-x1|<2,
又∵f(0)=f(2)=a>0,函数f(x)图象的对称轴x=1∈(0,2),
设f(x)=x2-2x+a<0的解集为(m,n),
则(m,n)⊆(0,2),
当t∈(m,n)⊆(0,2)时,
t+2∈(2,4),故f(t+2)>0,
| 2t+1 |
| 3 |
| 2m+1 |
| 3 |
| 2n+1 |
| 3 |
| 2t+1 |
| 3 |
故f(t+2)•f(
| 2t+1 |
| 3 |
即f(t+2)•f(
| 2t+1 |
| 3 |
故答案为:负.
点评:本题考查的知识点是二次函数的图象和性质,其中根据已知分析出f(t+2),f(
)的符号,是解答的关键.
| 2t+1 |
| 3 |

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
已知集合M={x|-1<x<1},N={x|3x>1},则M∩N=( )
| A、∅ |
| B、{x|x>0} |
| C、{x|x<1} |
| D、{x|0<x<1} |
已知点P为三棱锥O-ABC的底面ABC所在平面内的一点,且
=
+k
-
,则实数k的值为( )
| OP |
| 1 |
| 2 |
| OA |
| OB |
| OC |
A、-
| ||
B、
| ||
| C、1 | ||
D、
|
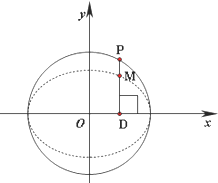 如图,在圆x2+y2=2上任取一点P,过点P作x轴的垂线段PD,D为垂足.点M在线段DP上,且
如图,在圆x2+y2=2上任取一点P,过点P作x轴的垂线段PD,D为垂足.点M在线段DP上,且
 某几何体的三视图如图所示,其俯视图是中心角为60°的扇形,则该几何体的体积为
某几何体的三视图如图所示,其俯视图是中心角为60°的扇形,则该几何体的体积为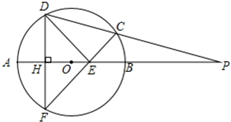 如图,P是⊙O的直径AB延长线上一点,割线PCD交⊙O于C、D两点,弦DF与直径AB垂直,H为垂足,CF与AB交于点E.
如图,P是⊙O的直径AB延长线上一点,割线PCD交⊙O于C、D两点,弦DF与直径AB垂直,H为垂足,CF与AB交于点E.