题目内容
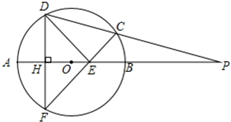 如图,P是⊙O的直径AB延长线上一点,割线PCD交⊙O于C、D两点,弦DF与直径AB垂直,H为垂足,CF与AB交于点E.
如图,P是⊙O的直径AB延长线上一点,割线PCD交⊙O于C、D两点,弦DF与直径AB垂直,H为垂足,CF与AB交于点E.(Ⅰ)求证:PA•PB=PO•PE;
(Ⅱ)若DE⊥CF,∠P=15°,⊙O的半径为2,求弦CF的长.
考点:与圆有关的比例线段
专题:直线与圆
分析:(Ⅰ)由已知条件推导出△PDO∽△PEC,从而得到PD•PC=PO•PE,由切割线定理,得PA•PB=PD•PC,由此能证明PA•PB=PO•PE.
(Ⅱ)由图可知,CF=CE+EF,而由垂径定理可知DE=EF,所以只要求出DE和CE即可,欲求CE,可通过证明△DHO∽△DEC,运用比例线段进行求解,至于DE,则根据题中给出的已知条件可说明三角形DHE为等腰直角三角形,而DH和HE则可通过勾股定理求出,从而求出CF的值.
(Ⅱ)由图可知,CF=CE+EF,而由垂径定理可知DE=EF,所以只要求出DE和CE即可,欲求CE,可通过证明△DHO∽△DEC,运用比例线段进行求解,至于DE,则根据题中给出的已知条件可说明三角形DHE为等腰直角三角形,而DH和HE则可通过勾股定理求出,从而求出CF的值.
解答:
(Ⅰ)证明:连结OD,∵AB是圆O的直径,
弦DF与直径AB垂直,H为垂足,C在圆O上,
∴∠DOA=∠DCF,∠POD=∠PCE,
又∵∠DPO=∠EPC,∴△PDO∽△PEC,
∴
=
,∴PD•PC=PO•PE,
由切割线定理,得PA•PB=PD•PC,
∴PA•PB=PO•PE.
(Ⅱ)解:由(Ⅰ)知:AB是弦DF的垂直平分线,
∴DE=EF.∴∠DEA=∠FEA.
∵DE⊥CF,∴∠DEA=∠FEA=45°.∴∠FEA=∠CEP=45°.
∵∠P=15°,∴∠AOD=60°.
在Rt△DHO中∵∠AOD=60°,OD=2,
∴OH=1,DH=
.
∵△DHE是等腰直角三角形,∴DE=
.
又∵∠AOD=∠DCF,∠DHO=∠DEC=90°,
∴△DHO∽△DEC.∴
=
.
∴
=
.∴EC=
.
∴CF=CE+EF=CE+DE=
+
.

弦DF与直径AB垂直,H为垂足,C在圆O上,
∴∠DOA=∠DCF,∠POD=∠PCE,
又∵∠DPO=∠EPC,∴△PDO∽△PEC,
∴
| PD |
| PE |
| PO |
| PC |
由切割线定理,得PA•PB=PD•PC,
∴PA•PB=PO•PE.
(Ⅱ)解:由(Ⅰ)知:AB是弦DF的垂直平分线,
∴DE=EF.∴∠DEA=∠FEA.
∵DE⊥CF,∴∠DEA=∠FEA=45°.∴∠FEA=∠CEP=45°.
∵∠P=15°,∴∠AOD=60°.
在Rt△DHO中∵∠AOD=60°,OD=2,
∴OH=1,DH=
| 3 |
∵△DHE是等腰直角三角形,∴DE=
| 6 |
又∵∠AOD=∠DCF,∠DHO=∠DEC=90°,
∴△DHO∽△DEC.∴
| DH |
| DE |
| HO |
| EC |
∴
| ||
|
| 1 |
| EC |
| 2 |
∴CF=CE+EF=CE+DE=
| 2 |
| 6 |
点评:本题考查线段乘积相等的证明,考查线段长的求法,解题时要认真审题,注意切割线定理的合理运用.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
若关于x的不等式mx-2>0的解集是{x|x>2},则实数m等于( )
| A、-1 | B、-2 | C、1 | D、2 |
不等式组
表示的平面区域是下列图中的( )
|
A、 |
B、 |
C、 |
D、 |
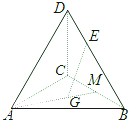 如图,四面体ABCD中,G为△ABC的重心,
如图,四面体ABCD中,G为△ABC的重心,