题目内容
15.要得到函数y=-cos2x的图象,只需将函数y=sin(2x-$\frac{π}{4}$)的图象( )| A. | 向右平移$\frac{π}{8}$个单位 | B. | 向左平移$\frac{π}{8}$个单位 | ||
| C. | 向左平移$\frac{π}{4}$个单位 | D. | 向右平移$\frac{π}{4}$个单位 |
分析 由条件利用诱导公式,以及函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答 解:∵y=sin(2x-$\frac{π}{4}$)=cos($\frac{π}{2}$-2x+$\frac{π}{4}$)=cos2(x-$\frac{3π}{8}$),
y=-cos2x=cos(π-2x)=cos2(x-$\frac{π}{2}$)=cos2(x-$\frac{3π}{8}$-$\frac{π}{8}$),
∴要得到函数y=-cos2x的图象,只需将函数y=sin(2x-$\frac{π}{4}$)的图象向右平移$\frac{π}{8}$个单位.
故选:A.
点评 本题主要考查诱导公式的应用,函数y=Asin(ωx+φ)的图象变换规律,统一这两个三角函数的名称,是解题的关键,属于基础题.

练习册系列答案
相关题目
5.公比为2的等比数列{an} 的各项都是正数,且a3a11=16,则a5=( )
| A. | 4 | B. | 2 | C. | 1 | D. | 8 |
6.抛物线y2=2px上横坐标为4的点到此抛物线焦点的距离为9,则该抛物线的焦点到准线的距离为( )
| A. | 4 | B. | 9 | C. | 10 | D. | 18 |
3.已知倾斜角为θ的直线,与直线x-3y+1=0垂直,则$\frac{2}{{3{{sin}^2}θ-{{cos}^2}θ}}$=( )
| A. | $\frac{10}{3}$ | B. | 一$\frac{10}{3}$ | C. | $\frac{10}{13}$ | D. | 一$\frac{10}{13}$ |
20.点P在边长为2的正方形ABCD内运动,则动点P到定点A的距离|PA|<1的概率为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{16}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{16}$ |
5.“a<2”是“实系数一元二次方程x2+ax+1=0有虚根”的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
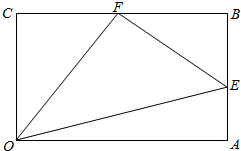 如图,某地要在矩形区域OABC内建造三角形池塘OEF,E,F分别在AB,BC边上,OA=5米,OC=4米,∠EOF=$\frac{π}{4}$,设CF=x,AE=y.
如图,某地要在矩形区域OABC内建造三角形池塘OEF,E,F分别在AB,BC边上,OA=5米,OC=4米,∠EOF=$\frac{π}{4}$,设CF=x,AE=y.