题目内容
函数y=（
）x2-2的单调递减区间为（ ）
| 1 |
| 2 |
| A、（-∞，0] | ||
| B、[0，+∞） | ||
C、（-∞，
| ||
D、[
|
考点：函数的单调性及单调区间
专题：计算题,函数的性质及应用
分析：令t=x2-2，则y=（
）t，即有y在t∈R上递减，由复合函数的单调性：同增异减，求出二次函数的增区间即可．
| 1 |
| 2 |
解答：
解：令t=x2-2，
则y=（
）t，即有y在t∈R上递减，
由于t在x∈[0，+∞）上递增，
则由复合函数的单调性，可知，
函数y的单调减区间为：[0，+∞）．
故选B．
则y=（
| 1 |
| 2 |
由于t在x∈[0，+∞）上递增，
则由复合函数的单调性，可知，
函数y的单调减区间为：[0，+∞）．
故选B．
点评：本题考查复合函数的单调性：同增异减，考查二次函数和指数函数的单调性，属于中档题和易错题．
练习册系列答案
相关题目
函数y=3sin（3x+
）-3的最小正周期为（ ）
| π |
| 3 |
A、
| ||
B、
| ||
| C、3π | ||
D、
|
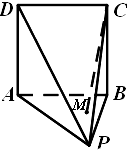如图，四棱锥P-ABCD的底面ABCD是边长为1的正方形，面PAB⊥面ABCD．在面PAB内的有一个动点M，记M到面PAD的距离为d．若|MC|2-d2=1，则动点M在面PAB内的轨迹是（ ）| A、圆的一部分 |
| B、椭圆的一部分 |
| C、双曲线的一部分 |
| D、抛物线的一部分 |
函数f（x）=7+ax-3（a＞0，a≠1）的图象恒过定点P，则定点P的坐标是（ ）
| A、（3，3） |
| B、（3，2） |
| C、（3，8） |
| D、（3，7） |
函数f（x）=
的定义域（ ）
| 1-x |
| A、（-∞，0） |
| B、（-∞，0] |
| C、（0，+∞） |
| D、（-∞，1] |