题目内容
若数列{an}满足:a1=
,a2=2,3(an+1-2an+an-1)=2,
(1)证明:数列{an+1-an}是等差数列;
(2)求使
+
+
+…+
>
成立的最小正整数n.
| 2 |
| 3 |
(1)证明:数列{an+1-an}是等差数列;
(2)求使
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
| 5 |
| 2 |
考点:数列与不等式的综合
专题:等差数列与等比数列
分析:(1)令bn=an+1-an,则bn-1=an-an-1,由已知得(an+1-an)-(an-an-1)=
,由此能证明数列{an+1-an}是首项为
,公差为
的等差数列.
(2)由an+1-an=
+(n-1)•
=
(n+1),利用累加法得an=
+
(2+3+4+…+n)=
,从而
=
=3(
-
),由此利用裂项法能求出使
+
+
+…+
>
成立的最小正整数n.
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
(2)由an+1-an=
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| n2+n |
| 3 |
| 1 |
| an |
| 3 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
| 5 |
| 2 |
解答:
(1)证明:令bn=an+1-an,
则bn-1=an-an-1,
∵3(an+1-2an+an-1)=2,
∴an+1-2an+an-1=
,
∴an+1-an-an+an-1=
,
(an+1-an)-(an-an-1)=
,
∴bn-bn-1=
,
又a2-a1=2-
=
,
∴数列{an+1-an}是首项为
,公差为
的等差数列.
(2)解:由(1)得an+1-an=
+(n-1)•
=
(n+1),
∴an=a1+a2-a1+a3-a2+…+an-an-1
=
+
(2+3+4+…+n)
=
,
∴
=
=3(
-
),
∴
+
+
+…+
=3(1-
+
-
+…+
-
)
=3(1-
)
=
,
∵
+
+
+…+
>
,
∴
>
,
解得n>5,
又n为正整数,∴n最小为6.
则bn-1=an-an-1,
∵3(an+1-2an+an-1)=2,
∴an+1-2an+an-1=
| 2 |
| 3 |
∴an+1-an-an+an-1=
| 2 |
| 3 |
(an+1-an)-(an-an-1)=
| 2 |
| 3 |
∴bn-bn-1=
| 2 |
| 3 |
又a2-a1=2-
| 2 |
| 3 |
| 4 |
| 3 |
∴数列{an+1-an}是首项为
| 4 |
| 3 |
| 2 |
| 3 |
(2)解:由(1)得an+1-an=
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
∴an=a1+a2-a1+a3-a2+…+an-an-1
=
| 2 |
| 3 |
| 2 |
| 3 |
=
| n2+n |
| 3 |
∴
| 1 |
| an |
| 3 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
=3(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=3(1-
| 1 |
| n+1 |
=
| 3n |
| n+1 |
∵
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
| 5 |
| 2 |
∴
| 3n |
| n+1 |
| 5 |
| 2 |
解得n>5,
又n为正整数,∴n最小为6.
点评:本题考查等差数列的证明,考查满足条件的最上正整数n的求法,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
相关题目
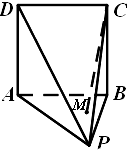 如图,四棱锥P-ABCD的底面ABCD是边长为1的正方形,面PAB⊥面ABCD.在面PAB内的有一个动点M,记M到面PAD的距离为d.若|MC|2-d2=1,则动点M在面PAB内的轨迹是( )
如图,四棱锥P-ABCD的底面ABCD是边长为1的正方形,面PAB⊥面ABCD.在面PAB内的有一个动点M,记M到面PAD的距离为d.若|MC|2-d2=1,则动点M在面PAB内的轨迹是( )| A、圆的一部分 |
| B、椭圆的一部分 |
| C、双曲线的一部分 |
| D、抛物线的一部分 |
函数f(x)=7+ax-3(a>0,a≠1)的图象恒过定点P,则定点P的坐标是( )
| A、(3,3) |
| B、(3,2) |
| C、(3,8) |
| D、(3,7) |
函数f(x)=
的定义域( )
| 1-x |
| A、(-∞,0) |
| B、(-∞,0] |
| C、(0,+∞) |
| D、(-∞,1] |
直线l不经过坐标原点O,且与椭圆
+y2=1交于A、B两点,M是线段AB的中点.那么,直线AB与直线OM的斜率之积为( )
| x2 |
| 2 |
| A、-1 | ||
| B、1 | ||
C、-
| ||
| D、2 |
将边长为a的正方形沿对角线AC折起,使得BD=a,则三棱锥D-ABC的体积为( )
| A、6a3 | ||||
| B、12a3 | ||||
C、
| ||||
D、
|