题目内容
18.已知$\left\{{\sqrt{a_n}}\right\}$是等比数列,a1=1,a2=2,则{an}的前5项和为( )| A. | 31 | B. | 30 | C. | $31\sqrt{2}$ | D. | $30\sqrt{2}$ |
分析 根据题意求出∴an=2n-1,再根据前n项和公式计算即可
解答 解∵$\left\{{\sqrt{a_n}}\right\}$是等比数列,a1=1,a2=2,
∴q=$\frac{\sqrt{{a}_{2}}}{\sqrt{{a}_{1}}}$=$\sqrt{2}$,
∴$\sqrt{{a}_{n}}$=1×($\sqrt{2}$)n-1,
∴an=2n-1,
∴{an}的前5项和为$\frac{1-{2}^{5}}{1-2}$=31,
故选:A.
点评 本题考查了等比数列的通项公式和求和公式,属于基础题

练习册系列答案
相关题目
8.已知a=log23,b=log47,$c={0.3^{-\frac{3}{2}}}$,则a,b,c的大小关系为( )
| A. | b>a>c | B. | a>b>c | C. | c>a>b | D. | c>b>a |
6.命题“?x∈R,x2+x+1<0”的否定为( )
| A. | ?x∈R,x2+x+1≥0 | B. | ?x∉R,x2+x+1≥0 | ||
| C. | ?x0∉R,x02+x0+1<0 | D. | ?x0∈R,x02+x0+1≥0 |
3.设等比数列{an}中,a3=3,a4=9,若a1•a2•a3•…•an=344,则n=( )
| A. | 13 | B. | 12 | C. | 11 | D. | 10 |
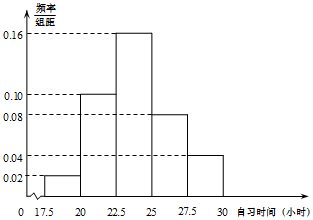 某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].则这200名学生中每周的自习时间不低于25小时的人数为( )
某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].则这200名学生中每周的自习时间不低于25小时的人数为( )