题目内容
11．函数y=$\frac{1+lnx}{1-lnx}$的图象大致为（ ）| A． |  | B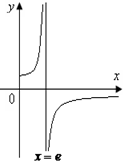． |  | C． |  | D． |  |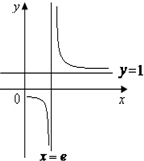
分析 原函数化简为y=-1+$\frac{2}{1-lnx}$，即可得到对称中心为（e，-1），于是可以判断C正确．
解答 解：y=$\frac{1+lnx}{1-lnx}$=-$\frac{1-lnx-2}{1-lnx}$=-1+$\frac{2}{1-lnx}$，
∴函数y=$\frac{1+lnx}{1-lnx}$的对称中心为（e，-1），
故选：C．
点评 本题考查了函数的图象的识别，关键是求出对称中心，属于基础题．
练习册系列答案
一线名师提优试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
2．已知f（x）=2|x|+x2+a-1有唯一的零点，则实数a的值为（ ）
| A． | -3 | B． | -2 | C． | -1 | D． | 0 |
16．下列函数中，既是偶函数又存在零点的是（ ）
| A． | y=x3 | B． | y=ex | C． | y=x2+1 | D． | y=ln|x| |
3．已知$U=\{x|\frac{x-2}{x}≤1\}$，A={x|2-x≤1}，则∁UA=（ ）
| A． | {x|x＜1} | B． | {x|0＜x＜1} | C． | {x|0≤x＜1} | D． | {x|x＞1} |
20．已知点A（4$\sqrt{3}$，1），将OA绕坐标原点O逆时针旋转$\frac{π}{6}$至OB，设C（1，0），∠COB=α，则tanα=（ ）
| A． | $\frac{{\sqrt{3}}}{12}$ | B． | $\frac{{\sqrt{3}}}{3}$ | C． | $\frac{{10\sqrt{3}}}{11}$ | D． | $\frac{{5\sqrt{3}}}{11}$ |