题目内容
20.已知点A(4$\sqrt{3}$,1),将OA绕坐标原点O逆时针旋转$\frac{π}{6}$至OB,设C(1,0),∠COB=α,则tanα=( )| A. | $\frac{{\sqrt{3}}}{12}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{10\sqrt{3}}}{11}$ | D. | $\frac{{5\sqrt{3}}}{11}$ |
分析 设直线OA的倾斜角为θ,则tanθ=$\frac{1}{4\sqrt{3}}$,再根据α=θ+$\frac{π}{6}$,求得tanα=tan(θ+$\frac{π}{6}$)的值.
解答 解:由题意,设直线OA的倾斜角为θ,则tanθ=$\frac{1}{4\sqrt{3}}$=$\frac{\sqrt{3}}{12}$,
α=θ+$\frac{π}{6}$,tanα=tan(θ+$\frac{π}{6}$)=$\frac{tanθ+tan\frac{π}{6}}{1-tanθ•tan\frac{π}{6}}$=$\frac{5\sqrt{3}}{11}$,
故选:D.
点评 本题主要考查任意角的三角函数的定义、两角和的正切公式的应用,属于基础题.

练习册系列答案
相关题目
15.设f(x)=lg$\frac{2+x}{2-x}$,则f(5x-3)的定义域为( )
| A. | (-$\frac{74}{25},22$) | B. | (-$\frac{74}{25},25$) | C. | (-2,2) | D. | (0,1) |
5.在△ABC中,若sinC(cosA+cosB)=sinA+sinB,则△ABC的形状是( )
| A. | 等腰三角形 | B. | 直角三角形 | ||
| C. | 等腰三角形或直角三角形 | D. | 等腰直角三角形 |
12.设变量x,y满足约束条件$\left\{\begin{array}{l}x≥0\\ y≥3x\\ x+ay≤7\end{array}\right.$,若目标函数z=x+y的最大值为14,则a值为( )
| A. | 1 | B. | $\frac{1}{2}$或$\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
9.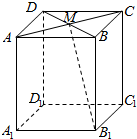 在长方体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是( )
在长方体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是( )
 在长方体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是( )
在长方体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是( )| A. | -$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | B. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | C. | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ | D. | -$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{c}$ |