题目内容
14．已知数列{an}是等差数列，其前n项和为Sn，a1+a5=0，S3+S5=-6，求an，Sn的表达式．分析 利用已知条件求出数列的第三项与第二项，即可求出首项与公差，然后求解即可．
解答 解：数列{an}是等差数列，其前n项和为Sn，a1+a5=0，可得a3=0，S5=5a3=0，
S3+S5=-6，可得S3=-6，所以a2=-2．d=2，a1=-4，
an=-4+（n-1）×2=2n-6．
Sn=-4n+$\frac{n（n-1）}{2}×2$=n2-5n．
点评 本题考查数列的性质，等差数列求和以及通项公式的求法，考查计算能力．
练习册系列答案
相关题目
4．cos$\frac{11}{4}$π的值为（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | -$\frac{\sqrt{2}}{2}$ |
5．甲、乙、丙三台机器是否需要维修相互之间没有影响，在一小时内甲、乙、丙三台机床需要维修的概率分别是0.1，0.2，0.4，则一小时内恰有一台机床需要维修的概率是（ ）
| A． | 0.444 | B． | 0.008 | C． | 0.7 | D． | 0.233 |
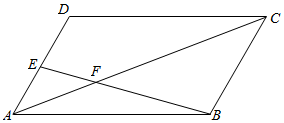如图，E是平行四边形ABCD的边AD上一点，且$\overrightarrow{AE}$=$\frac{1}{4}$$\overrightarrow{AD}$，F为BE与AC的交点，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{BC}$=$\overrightarrow{b}$，若$\overrightarrow{BF}$=k$\overrightarrow{BE}$，$\overrightarrow{AF}$=h$\overrightarrow{AC}$，则k=$\frac{4}{5}$，h=$\frac{1}{5}$．
6．设集合A={x|x2-4x+3＜0}，B={x|2x-3＞0}，则A∩B=（ ）
| A． | （-3，-$\frac{3}{2}$） | B． | （-3，$\frac{3}{2}$） | C． | （1，$\frac{3}{2}$） | D． | （$\frac{3}{2}$，3） |
3．设复数z满足z+i=3-i，则$\overline{z}$=（ ）
| A． | -1+2i | B． | 1-2i | C． | 3+2i | D． | 3-2i |
9．已知向量|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=1，且$\overrightarrow{a}$与$\overrightarrow{a}$+2$\overrightarrow{b}$的夹角为$\frac{π}{3}$，则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{2}$ | D． | $\frac{2π}{3}$ |