题目内容

5．甲、乙、丙三台机器是否需要维修相互之间没有影响，在一小时内甲、乙、丙三台机床需要维修的概率分别是0.1，0.2，0.4，则一小时内恰有一台机床需要维修的概率是（　　）
A．0.444B．0.008C．0.7D．0.233

分析 由已知条件利用对立事件概率计算公式和相互独立事件概率乘法公式能求出一小时内恰有一台机床需要维修的概率．

解答 解：∵甲、乙、丙三台机器是否需要维修相互之间没有影响，
在一小时内甲、乙、丙三台机床需要维修的概率分别是0.1，0.2，0.4，
∴一小时内恰有一台机床需要维修的概率是：
p=0.1×（1-0.2）×（1-0.4）+（1-0.1）×0.2×（1-0.4）+（1-0.1）×（1-0.2）×0.4=0.444．
故选：A．

点评 本题考查概率的求法，是中档题，解题时要认真审题，注意对立事件概率计算公式和相互独立事件概率乘法公式的合理运用．

练习册系列答案
相关题目
15．阅读如图所示的程序框图，当输出的结果S为0时，判断框中应填（　　）
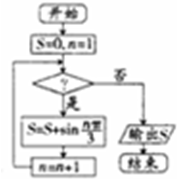
A．n≤4B．n≤5C．n≤7D．n≤8
16．已知全集U=R，A={x|log4x＜1}，B={x|-x2-2x+3＜0}，则A∩（CUB）为（　　）
A．[0，1]B．[-3，1]C．[1，4）D．（0，1]
13．已知数列{an}满足an+2-an+1=an+1-an（n∈N+），且a1008=$\frac{π}{2}$，若函数f（x）=sin2x+2cos2$\frac{x}{2}$，记yn=f（an），则数列{yn}的前2015项和为（　　）
A．2015B．-2015C．0D．1
20．执行如图的算法语句，则输出S为（　　）
A．$\frac{2015}{2016}$B．$\frac{4032}{2017}$C．$\frac{4030}{2016}$D．$\frac{2016}{2017}$
10．在△ABC中，内角A，B，C所对的边分别为a，b，c，b≠c，且sin2C-sin2B=$\sqrt{3}$sinBcosB-$\sqrt{3}$sinCcosC．
（1）求角A的大小；
（2）若a=$\sqrt{3}$，sinC=$\frac{3}{4}$，求△ABC的面积．
17．已知复数z=1+$\frac{2i}{1-i}$，则1+z+z2+…+z2016为（　　）
A．1+iB．1-iC．iD．1
14．已知数列{an}是等差数列，其前n项和为Sn，a1+a5=0，S3+S5=-6，求an，Sn的表达式．
15．已知A（2，5），B（4，1）．若点P（x，y）在线段AB上，则2x-y的最大值为（　　）
A．-1B．3C．7D．8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网