题目内容
2.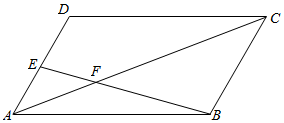 如图,E是平行四边形ABCD的边AD上一点,且$\overrightarrow{AE}$=$\frac{1}{4}$$\overrightarrow{AD}$,F为BE与AC的交点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,若$\overrightarrow{BF}$=k$\overrightarrow{BE}$,$\overrightarrow{AF}$=h$\overrightarrow{AC}$,则k=$\frac{4}{5}$,h=$\frac{1}{5}$.
如图,E是平行四边形ABCD的边AD上一点,且$\overrightarrow{AE}$=$\frac{1}{4}$$\overrightarrow{AD}$,F为BE与AC的交点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,若$\overrightarrow{BF}$=k$\overrightarrow{BE}$,$\overrightarrow{AF}$=h$\overrightarrow{AC}$,则k=$\frac{4}{5}$,h=$\frac{1}{5}$.
分析 根据向量加法、减法的几何意义便有$\overrightarrow{BF}=\overrightarrow{BA}+\overrightarrow{AF}=\overrightarrow{BA}+h\overrightarrow{AC}=\overrightarrow{BA}+h(\overrightarrow{BC}-\overrightarrow{BA})$,这样进行向量的数乘运算便可得出$\overrightarrow{BF}=(1-h)\overrightarrow{BA}+h\overrightarrow{BC}$,同样可得到$\overrightarrow{BF}=k\overrightarrow{BA}+\frac{k}{4}\overrightarrow{BC}$,这样由平面向量基本定理即可得到$\left\{\begin{array}{l}{1-h=k}\\{h=\frac{k}{4}}\end{array}\right.$,这样解出h,k即可.
解答 解:根据条件:
$\overrightarrow{BF}=\overrightarrow{BA}+\overrightarrow{AF}$
=$\overrightarrow{BA}+h\overrightarrow{AC}$
=$\overrightarrow{BA}+h(\overrightarrow{BC}-\overrightarrow{BA})$
=$(1-h)\overrightarrow{BA}+h\overrightarrow{BC}$;
又$\overrightarrow{BF}=k\overrightarrow{BE}$
=$k(\overrightarrow{BA}+\overrightarrow{AE})$
=$k(\overrightarrow{BA}+\frac{1}{4}\overrightarrow{AD})$
=$k\overrightarrow{BA}+\frac{k}{4}\overrightarrow{BC}$;
∴由平面向量基本定理得,$\left\{\begin{array}{l}{1-h=k}\\{h=\frac{k}{4}}\end{array}\right.$;
解得$k=\frac{4}{5},h=\frac{1}{5}$.
故答案为:$\frac{4}{5},\frac{1}{5}$.
点评 考查向量加法和减法的几何意义,以及向量的数乘运算,相等向量的概念,平面向量基本定理.

 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案(附:若随机变量ξ服从正态分布N(μ,σ2),且P(μ-σ<ξ<μ+σ)=68.26%,P(μ-2σ<ξ<μ+2σ)=95.44%)
| A. | 0.1588 | B. | 0.1587 | C. | 0.1586 | D. | 0.1585 |
| A. | 2015 | B. | -2015 | C. | 0 | D. | 1 |
| A. | 1+i | B. | 1-i | C. | i | D. | 1 |
| A. |  | B. |  | ||
| C. |  | D. |  |
| A. | 2 | B. | 6 | C. | 12 | D. | 3+2$\sqrt{2}$ |