题目内容
已知f(x)=cos2x-sin2x.
(1)求f(
)的值及f(x)的最大值;
(2)求f(x)的递减区间.
(1)求f(
| π |
| 4 |
(2)求f(x)的递减区间.
考点:二倍角的余弦,余弦函数的图象,三角函数的最值
专题:三角函数的图像与性质
分析:(1)利用二倍角的余弦可知f(x)=cos2x,从而可求f(
)的值及f(x)的最大值;
(2)利用余弦函数的单调性,由2kπ≤2x≤2kπ+π(k∈Z)即可求得f(x)的递减区间.
| π |
| 4 |
(2)利用余弦函数的单调性,由2kπ≤2x≤2kπ+π(k∈Z)即可求得f(x)的递减区间.
解答:
解:(1)∵f(x)=cos2x-sin2x=cos2x,
∴f(
)=cos
=0,f(x)max=1;
(2)由2kπ≤2x≤2kπ+π(k∈Z)得:kπ≤x≤kπ+
(k∈Z),
∴f(x)的递减区间为[kπ,kπ+
]k∈Z.
∴f(
| π |
| 4 |
| π |
| 2 |
(2)由2kπ≤2x≤2kπ+π(k∈Z)得:kπ≤x≤kπ+
| π |
| 2 |
∴f(x)的递减区间为[kπ,kπ+
| π |
| 2 |
点评:本题考查二倍角的余弦,着重考查余弦函数的单调性与最值,属于中档题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
已知F1,F2是双曲线
-
=1(a>0,b>0)的两个焦点,点P是该双曲线和圆x2+y2=a2+b2的一个交点,若sin∠PF1F2=2sin∠PF2F1,则该双曲线的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f(x)=-x3,则下列说话正确的是( )
| A、f(x)为奇函数,且在(0,+∞)上是增函数 |
| B、f(x)为奇函数,且在(0,+∞)上是减函数 |
| C、f(x)为偶函数,且在(0,+∞)上是增函数 |
| D、f(x)为偶函数,且在(0,+∞)上是偶函数 |
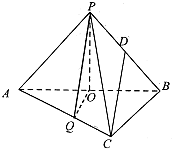 如图,三棱锥P-ABC中,已知平面PAB⊥平面ABC,AC⊥BC,AC=BC=2a,点O,D分别是AB,PB的中点,PO⊥AB,点Q在线段AC上,且AQ=2QC.
如图,三棱锥P-ABC中,已知平面PAB⊥平面ABC,AC⊥BC,AC=BC=2a,点O,D分别是AB,PB的中点,PO⊥AB,点Q在线段AC上,且AQ=2QC.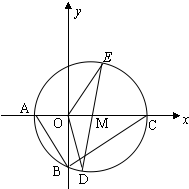 如图,△ABC中,
如图,△ABC中,