题目内容
若△ABC三边长a,b,c满足等式(a+b-c)(a+b+c)=ab,则角C的大小为 .
考点:余弦定理
专题:三角函数的求值
分析:已知的等式左边利用平方差公式及完全平方公式化简,整理后得到关系式,再利用余弦定理表示出cosC,将得出的关系式代入求出cosC的值,即可确定出C的度数.
解答:
解:∵(a+b-c)(a+b+c)=(a+b)2-c2=a2+b2-c2+2ab=ab,即a2+b2-c2=-ab,
∴cosC=
=
=-
,
∵C为三角形内角,
∴C=
.
故答案为:
∴cosC=
| a2+b2-c2 |
| 2ab |
| -ab |
| 2ab |
| 1 |
| 2 |
∵C为三角形内角,
∴C=
| 2π |
| 3 |
故答案为:
| 2π |
| 3 |
点评:此题考查了余弦定理,以及特殊角的三角函数值,熟练掌握余弦定理是解本题的关键.

练习册系列答案
相关题目
已知函数f(x)=-x3,则下列说话正确的是( )
| A、f(x)为奇函数,且在(0,+∞)上是增函数 |
| B、f(x)为奇函数,且在(0,+∞)上是减函数 |
| C、f(x)为偶函数,且在(0,+∞)上是增函数 |
| D、f(x)为偶函数,且在(0,+∞)上是偶函数 |
半径为R的球面上有A、B两点,它们的球面距离是
R,则线段AB的长为( )
| π |
| 2 |
A、
| ||||
| B、R | ||||
C、
| ||||
D、
|
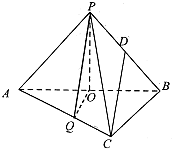 如图,三棱锥P-ABC中,已知平面PAB⊥平面ABC,AC⊥BC,AC=BC=2a,点O,D分别是AB,PB的中点,PO⊥AB,点Q在线段AC上,且AQ=2QC.
如图,三棱锥P-ABC中,已知平面PAB⊥平面ABC,AC⊥BC,AC=BC=2a,点O,D分别是AB,PB的中点,PO⊥AB,点Q在线段AC上,且AQ=2QC.