题目内容
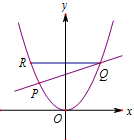 如图,设直线l:y=kx+
如图,设直线l:y=kx+| 2 |
(1)若点M是线段PQ的中点,求点M到x轴距离的最小值;
(2)当k>0时,过点Q作y轴的垂线交抛物线C于点R,若
| PQ |
| PR |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)把直线l的方程与抛物线方程联立可得根与系数的关系,再利用中点坐标公式和二次函数的性质即可得出;
(2)利用数量积运算和根与系数的关系即可得出.
(2)利用数量积运算和根与系数的关系即可得出.
解答:
解:(1)设P(x1,y1),Q(x2,y2),M(x0,y0).
由
消去y,整理得x2-kx-
=0,
∴x1+x2=k,x1x2=-
,
∴x0=
=
,y0=kx0+
=
+
≥
∴点M到x轴距离的最小值为
.
(2)由题意得R(-x2,y2),
∴
•
=(x2-x1,y2-y1)•(-x2-x1,y2-y1)=(x2-x1)(-x2-x1)+(y2-y1)2
=x12-x22+(y2-y1)2=y1-y2+(y2-y1)2=(y2-y1)(y2-y1-1)=0,
∵y1≠y2,
∴y2-y1=1,从而k(x2-x1)=1,故k2(x2-x1)2=1.
∴k2[(x2+x1)2-4x1x2]=1,k2(k2+4
)=1.
解得k2=3-2
=(
-1)2(负根舍去),
∵k>0,∴k=
-1,
∴直线l的方程为y=(
-1)x+
.
由
|
| 2 |
∴x1+x2=k,x1x2=-
| 2 |
∴x0=
| x1+x2 |
| 2 |
| k |
| 2 |
| 2 |
| k2 |
| 2 |
| 2 |
| 2 |
∴点M到x轴距离的最小值为
| 2 |
(2)由题意得R(-x2,y2),
∴
| PQ |
| PR |
=x12-x22+(y2-y1)2=y1-y2+(y2-y1)2=(y2-y1)(y2-y1-1)=0,
∵y1≠y2,
∴y2-y1=1,从而k(x2-x1)=1,故k2(x2-x1)2=1.
∴k2[(x2+x1)2-4x1x2]=1,k2(k2+4
| 2 |
解得k2=3-2
| 2 |
| 2 |
∵k>0,∴k=
| 2 |
∴直线l的方程为y=(
| 2 |
| 2 |
点评:本题考查了直线与抛物线相交问题转化为方程联立得到关于x的一元二次方程及其根与系数的关系、中点坐标公式和二次函数的性质、数量积运算等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
已知定义在R上的函数f(x)满足f(2-x)为奇函数,函数f(x+3)关于直线x=1对称,则下列式子一定成立的是( )
| A、f(x-2)=f(x) |
| B、f(x-2)=f(x+6) |
| C、f(x-2)•f(x+2)=1 |
| D、f(-x)+f(x+1)=0 |
 如图,在平面直角坐标系中,直线y=kx+b(k≠0)分别交双曲线
如图,在平面直角坐标系中,直线y=kx+b(k≠0)分别交双曲线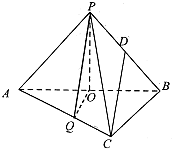 如图,三棱锥P-ABC中,已知平面PAB⊥平面ABC,AC⊥BC,AC=BC=2a,点O,D分别是AB,PB的中点,PO⊥AB,点Q在线段AC上,且AQ=2QC.
如图,三棱锥P-ABC中,已知平面PAB⊥平面ABC,AC⊥BC,AC=BC=2a,点O,D分别是AB,PB的中点,PO⊥AB,点Q在线段AC上,且AQ=2QC.