题目内容
4.点P在$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1上且到直线$\frac{x}{4}$+$\frac{y}{3}$=1的距离为$\frac{6}{5}$,则点P的个数为2.分析 求出与直线平行并且到直线$\frac{x}{4}$+$\frac{y}{3}$=1的距离为$\frac{6}{5}$的直线方程,然后利用直线与椭圆方程交点个数推出结果.
解答 解:点P在$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1上且到直线$\frac{x}{4}$+$\frac{y}{3}$=1的距离为$\frac{6}{5}$,
转化为与直线平行并且到直线$\frac{x}{4}$+$\frac{y}{3}$=1的距离为$\frac{6}{5}$的直线与椭圆的交点个数.
与直线平行并且到直线$\frac{x}{4}$+$\frac{y}{3}$=1的距离为$\frac{6}{5}$的直线方程为:3x+4y-6=0与3x+4y-18=0.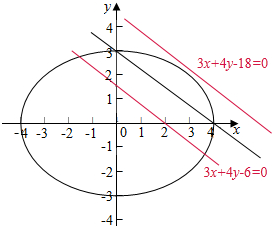
$\left\{\begin{array}{l}\frac{{x}^{2}}{16}+\frac{{y}^{2}}{9}=1\\ 3x+4y-18=0\end{array}\right.$,消去y可得:9x2+(3x-18)2=144.
化简可得:x2-6x+10=0,△=36-40=-4<0,方程无解,
直线3x+4y-6=0与椭圆必有2个交点.
故答案为:2.
点评 本题考查直线与椭圆的综合应用,平行线的求法转化思想的应用,考查分析问题解决问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知直线x-y+a=0与圆心为C的圆x2+y2+2$\sqrt{3}$x-4$\sqrt{3}$y+7=0相交于A,B两点,且$\overrightarrow{AC}$•$\overrightarrow{BC}$=4,则实数a的值为( )
| A. | $\sqrt{3}$或-$\sqrt{3}$ | B. | $\sqrt{3}$或3$\sqrt{3}$ | C. | $\sqrt{3}$或5$\sqrt{3}$ | D. | 3$\sqrt{3}$或5$\sqrt{3}$ |
12.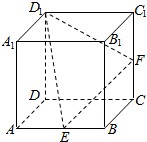 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是AB,CC1的中点,过点E,F1D1的截面与正方体的下底面相交于直线l,
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是AB,CC1的中点,过点E,F1D1的截面与正方体的下底面相交于直线l,
①请画出直线l的位置;
②设l∩BC=G,求BG的长.
 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是AB,CC1的中点,过点E,F1D1的截面与正方体的下底面相交于直线l,
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是AB,CC1的中点,过点E,F1D1的截面与正方体的下底面相交于直线l,①请画出直线l的位置;
②设l∩BC=G,求BG的长.
9.设集合M={x|0≤x<2},N={x|x-3<0},则M∩N=( )
| A. | {x|0≤x<1} | B. | {x|0≤x≤1} | C. | {x|0≤x<2} | D. | {x|0≤x≤2} |