题目内容
1.已知直线x-y+a=0与圆心为C的圆x2+y2+2$\sqrt{3}$x-4$\sqrt{3}$y+7=0相交于A,B两点,且$\overrightarrow{AC}$•$\overrightarrow{BC}$=4,则实数a的值为( )| A. | $\sqrt{3}$或-$\sqrt{3}$ | B. | $\sqrt{3}$或3$\sqrt{3}$ | C. | $\sqrt{3}$或5$\sqrt{3}$ | D. | 3$\sqrt{3}$或5$\sqrt{3}$ |
分析 圆x2+y2+2$\sqrt{3}$x-4$\sqrt{3}$y+7=0,可化为(x+$\sqrt{3}$)2+(y-2$\sqrt{3}$)2=8.利用$\overrightarrow{AC}$•$\overrightarrow{BC}$=4,可得∠ACB=60°,圆心到直线的距离为$\sqrt{6}$,即可得出结论.
解答 解:圆x2+y2+2$\sqrt{3}$x-4$\sqrt{3}$y+7=0,可化为(x+$\sqrt{3}$)2+(y-2$\sqrt{3}$)2=8.
∵$\overrightarrow{AC}$•$\overrightarrow{BC}$=4,∴2$\sqrt{2}$•2$\sqrt{2}$cos∠ACB=4
∴cos∠ACB=$\frac{1}{2}$,
∴∠ACB=60°
∴圆心到直线的距离为$\sqrt{6}$,
∴$\frac{|-\sqrt{3}-2\sqrt{3}+a|}{\sqrt{2}}$=$\sqrt{6}$,
∴a=$\sqrt{3}$或5$\sqrt{3}$.
故选:C.
点评 本题考查直线与圆的位置关系,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知球O半径为$\sqrt{5}$,设S、A、B、C是球面上四个点,其中∠ABC=120°,AB=BC=2,平面SAC⊥平面ABC,则棱锥S-ABC的体积的最大值为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | 3$\sqrt{3}$ |
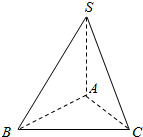 如图所示,在三棱锥S-ABC中,△ABC,△SBC都是等边三角形,且BC=1,SA=$\frac{\sqrt{3}}{2}$,则二面角S-BC-A的大小为60°.
如图所示,在三棱锥S-ABC中,△ABC,△SBC都是等边三角形,且BC=1,SA=$\frac{\sqrt{3}}{2}$,则二面角S-BC-A的大小为60°.