题目内容
9．设集合M={x|0≤x＜2}，N={x|x-3＜0}，则M∩N=（ ）| A． | {x|0≤x＜1} | B． | {x|0≤x≤1} | C． | {x|0≤x＜2} | D． | {x|0≤x≤2} |
分析 直接利用集合的交集的求法，求解即可．
解答 解：集合M={x|0≤x＜2}，N={x|x-3＜0}={x|x＜3}，
则M∩N={x|0≤x＜2}．
故选：C．
点评 本题考查集合的基本运算，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
5．
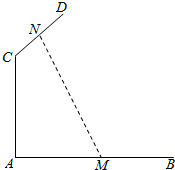如图，AB、CD为互相垂直的两异面直线，AC⊥AB，AC⊥CD，线段AC长为2，M∈AB，N∈CD，P为MN中点，且线段MN长为4，则点P的轨迹所形成的面积为（ ）
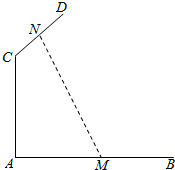如图，AB、CD为互相垂直的两异面直线，AC⊥AB，AC⊥CD，线段AC长为2，M∈AB，N∈CD，P为MN中点，且线段MN长为4，则点P的轨迹所形成的面积为（ ）| A． | 0 | B． | 3π | C． | 16π | D． | 8π |
1．已知函数f（x）是函数y=logax（a＞0且a≠1）的反函数，则函数y=f（x）+2图象恒过点的坐标为（ ）
| A． | （1，0） | B． | （0，1） | C． | （1，2） | D． | （0，3） |
19．从1，2，3，4，5，6，7，8，9中任取七个不同的数，则这七个数的平均数是5的概率为（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{9}$ | D． | $\frac{1}{8}$ |