题目内容
14.已知△ABC三顶点分别为A(1,3),B(3,1),C(-1,0),则AB边上的中线所在直线的一般式方程为2x-3y+2=0.分析 求出AB的中点,结合C点坐标,代入两点式方程,可得答案
解答 解:∵△ABC的三个顶点为A(1,3)、B(3,1)、C(-1,0),
∴AB的中点坐标为(2,2),
∴三角形AB边上中线所在直线的方程为:$\frac{y-2}{0-2}$=$\frac{x-2}{-1-2}$,
即:2x-3y+2=0,
故答案为:2x-3y+2=0.
点评 本题考查直线方程的求法,是基础题.解题时要认真审题,注意两点式方程的灵活运用.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
19.从1,2,3,4,5,6,7,8,9中任取七个不同的数,则这七个数的平均数是5的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{8}$ |
3.椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(0<b<a)$的右焦点到原点的距离和到右准线的距离相等,则该椭圆的离心率为( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
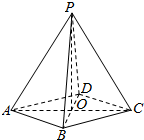 如图,在四棱锥P-ABCD中,底面ABCD是菱形,AC∩BD=O.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,AC∩BD=O.
 已知AB、DE为圆O的直径,CD⊥AB于N,N为OB的中点,EB与CD相交于点M,切线EF与DC的延长线交于点F.
已知AB、DE为圆O的直径,CD⊥AB于N,N为OB的中点,EB与CD相交于点M,切线EF与DC的延长线交于点F.