题目内容
20．椭圆$\frac{x^2}{16}$+$\frac{y^2}{12}$=1的离心率为$\frac{1}{2}$．分析 由椭圆的标准方程可得a、b的值，进而由a、b、c的关系式可得c的值，由椭圆离心率的计算公式计算可得答案．
解答 解：根据题意，椭圆的方程为$\frac{x^2}{16}$+$\frac{y^2}{12}$=1，其中a=$\sqrt{16}$=4，b=$\sqrt{12}$=2$\sqrt{3}$，
则c=$\sqrt{16-12}$=2，
则其离心率e=$\frac{c}{a}$=$\frac{2}{4}$=$\frac{1}{2}$；
故答案为：$\frac{1}{2}$．
点评 本题考查椭圆的简单几何性质，掌握椭圆的标准方程求出a、b、c的值以及离心率的计算公式是解题的关键．
练习册系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
11．已知球O半径为$\sqrt{5}$，设S、A、B、C是球面上四个点，其中∠ABC=120°，AB=BC=2，平面SAC⊥平面ABC，则棱锥S-ABC的体积的最大值为（ ）
| A． | $\frac{2\sqrt{3}}{3}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\sqrt{3}$ | D． | 3$\sqrt{3}$ |
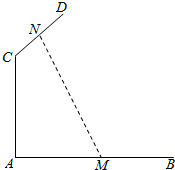如图，AB、CD为互相垂直的两异面直线，AC⊥AB，AC⊥CD，线段AC长为2，M∈AB，N∈CD，P为MN中点，且线段MN长为4，则点P的轨迹所形成的面积为（ ）