题目内容
已知等比数列{an}的前n项和为Sn，且S1，S2+a2，S3成等差数列，则数列{an}的公比为（ ）
| A、1 | ||
| B、2 | ||
C、
| ||
| D、3 |
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：利用等比数列的前n项和公式表示出S1，S2，S3，然后根据S1，S2+a2，S3成等差数列，利用等差数列的性质列出关系式，将表示出的S1，S2，S3代入得到关于a1与q的关系式，由a1≠0，两边同时除以a1，得到关于q的方程，求出方程的解，即可得到公比q的值．
解答：
解：∵S1，S2+a2，S3成等差数列，
∴2（S2+a2）=S1+S3，又数列{an}为等比数列，
∴2（a1+2a1q）=a1+（a1+a1q+a1q2），
整理得：a1q2-3a1q=0，
又a1≠0，∴q2-3q=0，
∵q≠0，解得：q=3．
故选：D．
∴2（S2+a2）=S1+S3，又数列{an}为等比数列，
∴2（a1+2a1q）=a1+（a1+a1q+a1q2），
整理得：a1q2-3a1q=0，
又a1≠0，∴q2-3q=0，
∵q≠0，解得：q=3．
故选：D．
点评：此题考查了等差数列的性质，等比数列的通项公式、求和公式，熟练掌握公式及性质是解本题的关键．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
若函数f（x）=x2+x-a，则使得“函数y=f（x）在区间（-1，1）内有零点”成立的一个必要非充分条件是（ ）
A、-
| ||
B、-
| ||
| C、0＜a＜2 | ||
D、-
|
将函数f（x）=
sin2x+
cos2x的图象向右平移
个单位，再把横坐标扩大到原来的2倍得到函数y=g（x）的图象，下面结论正确的是（ ）
| 2 |
| 6 |
| π |
| 4 |
A、函数y=g（x）在[0，
| ||
B、函数y=g（x）图象的一个对称中心为（
| ||
C、函数y=g（x+φ）为偶函数时，其中一个φ=-
| ||
D、函数y=g（x）图象关于直线x=
|
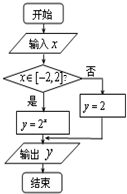
阅读程序框图（如图），如果输出的函数值在区间[
，1]上，则输入的实数x的取值范围是（ ）
| 1 |
| 4 |
| A、（-∞，-2] |
| B、[-2，0] |
| C、[0，2] |
| D、[2，+∞） |
在长为10cm的线段AB上任取一点C，现作一个矩形，邻边长分别等于线段AC、CB的长，则该矩形的面积大于24cm2的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合A=（-1，2），集合B={x|-x2-2x+3＞0}，则A∪B=（ ）
| A、（-1，1） |
| B、（-3，2） |
| C、（-1，3） |
| D、（-1，2） |
已知f（x）=ax和g（x）=bx是指数函数，则“f（2）＞g（2）”是“a＞b”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |